Eigentlich ist ein Dreieck nichts weiter als eine Menge von drei Punkten in der Ebene – seinen Eckpunkten. Aber die klassische Geometrie kennt eine Fülle von Objekten, die man aus diesen drei Punkten konstruieren kann, sowie von Beziehungen dieser Objekte untereinander. Beispiele sind die speziellen Punkte aus der Schulgeometrie, in denen sich bemerkenswerterweise jeweils drei gleichartige Geraden schneiden: die Mittelsenkrechten, die Winkelhalbierenden, die Höhen und die Seitenhalbierenden.

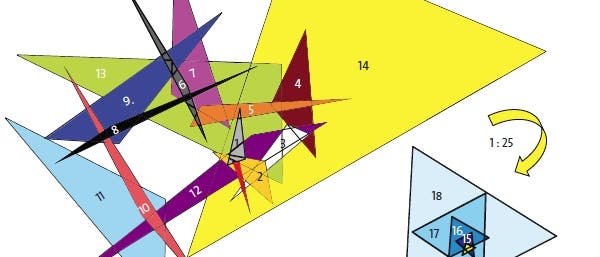
Entsprechend viele Möglichkeiten gibt es, aus einem Dreieck ein anderes zu machen. Man kann zum Beispiel als Eckpunkte des neuen Dreiecks die Mittelpunkte der Seiten des alten nehmen. Oder die "Fußpunkte" der Winkelhalbierenden – das sind die Punkte, an denen eine Winkelhalbierende die gegenüberliegende Seite trifft. Oder die Fußpunkte der Höhen, also der Senkrechten von einem Eckpunkt auf die gegenüberliegende Seite oder deren Verlängerung.

Jede dieser Vorschriften, aus einem Dreieck ein neues zu konstruieren, ist eine Abbildung ("Funktion") im mathematischen Sinn, und zwar von der Menge aller Dreiecke in dieselbe Menge. Auf das neue Dreieck kann man dieselbe Vorschrift wieder anwenden, auf das so entstandene Dreieck noch einmal, und so weiter – im Prinzip unendlich oft; man nennt das "die Abbildung iterieren". Und schon gerät die biedere Zirkel- und -Lineal-Konstruktionsvorschrift in Verbindung mit einem sehr modernen Teilgebiet der Mathematik...