Der Satz von Viviani: Die Summe der Lote von einem Punkt auf die Seiten eines gleichseitigen Dreiecks, mit den richtigen Vorzeichen gerechnet, ist konstant.

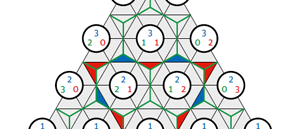
Zeichnen Sie bitte ein gleichseitiges Dreieck ABC der Seitenlänge g und in der gleichen Ebene irgendeinen Punkt P. Konstruieren Sie die Lote von P auf die drei Seiten BC, CA und AB. Deren Längen a, b und c versehen wir mit dem positiven Vorzeichen, wenn P auf der gleichen Seite wie die restliche Ecke des Dreiecks liegt, andernfalls mit dem negativen. Für Punkte im Inneren sind somit alle drei positiv, für Punkte auf einer Seite oder ihrer Verlängerung ist ein Wert gleich null, für eine der drei Ecken sind es zwei, und der dritte ist dann gleich der Länge h der Höhe von ABC.

Der Satz von Viviani besagt nun in seiner erweiterten Form, die auch negative Werte zulässt, dass die Summe a + b + c nicht von der Wahl des Punkts abhängt, sondern stets gleich h ist. Zum Beweis betrachten wir die Flächen der Dreiecke PAB, PBC und PCA mit entsprechenden Vorzeichen als halbe Produkte aus g und den zugehörigen Loten und addieren sie auf. Für die Dreiecksfläche ergibt sich gh/2 = (a + b + c)g/2. Der Satz lässt sich auf höhere Dimensionen verallgemeinern: Die Summe der n vorzeichenbehafteten Abstände eines Punkts von den Randpolytopen der...