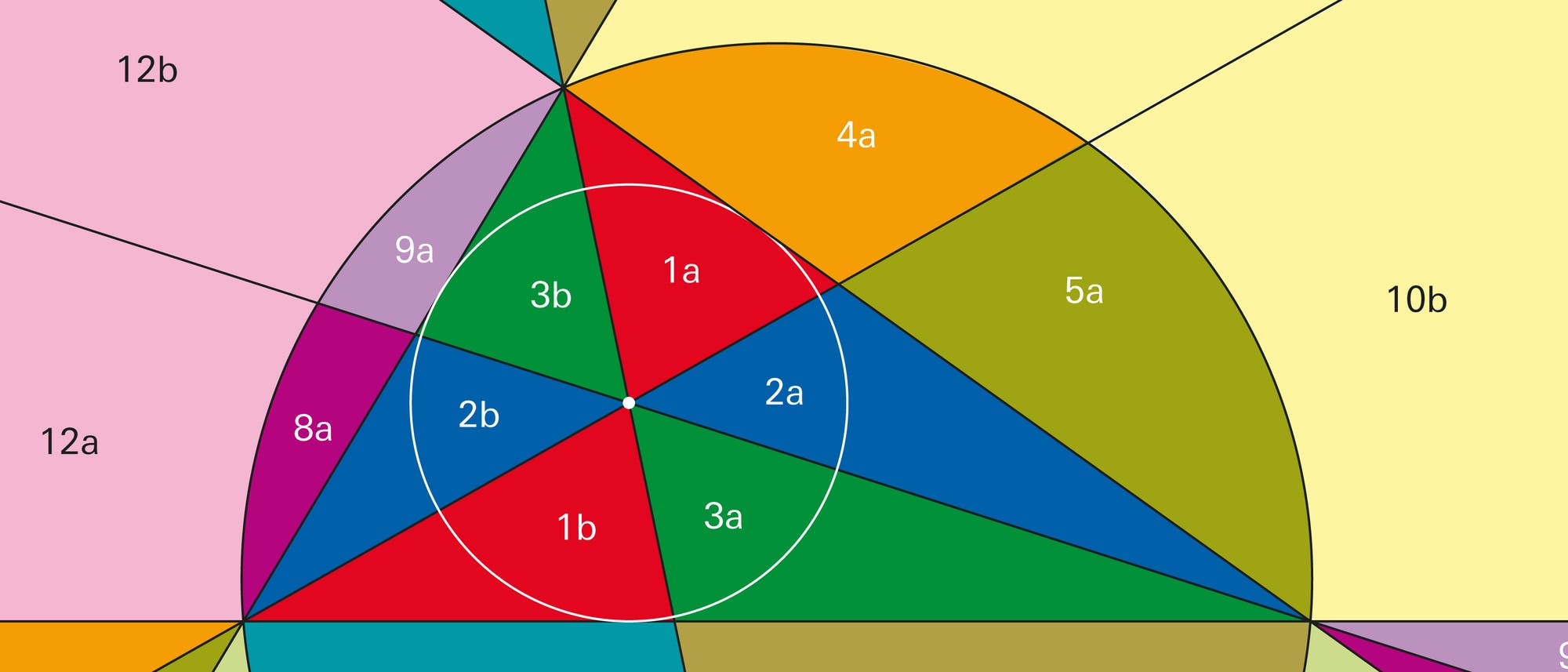
Besondere Punkte im Dreieck – das weckt fast unweigerlich Gedanken an die 9. Klasse. Da gibt es den Umkreis, den Inkreis und den Schwerpunkt eines beliebigen Dreiecks, den Schnittpunkt der Höhen nicht zu vergessen. Jedes Mal sollen sich eigentlich drei Geraden in einem Punkt treffen, verfehlen diesen Treffpunkt aber nur allzu häufig, weil die geheiligten Konstruktionswerkzeuge Zirkel und Lineal immer im falschen Moment wegrutschen oder der Bleistift nicht richtig gespitzt ist. Vor allem aber will das nagende Gefühl nicht weichen, dass nicht nur das Gerät hoffnungslos veraltet ist, sondern das ganze Thema. Und schon kommt die nächste Frage um die Ecke: "Gibt es in der Geometrie – oder überhaupt in der Mathematik – noch etwas Neues?"

Die Antwort – wenig überraschend für regelmäßige Leser dieser Rubrik – lautet Ja. Und was die besonderen Punkte im Dreieck angeht, ist die Flut an Neuigkeiten sogar überwältigend. Clark Kimberling, Mathematikprofesor an der University of Evansville (Indiana), führt im Internet eine Liste dieser Punkte und ihrer Beziehungen zueinander, beginnend mit X(1), dem Inkreismittelpunkt, in dem sich alle drei Winkelhalbierenden treffen. Und die ist in den letzten sieben Jahren immerhin von 3587 auf 13463 Einträge angewachsen ...