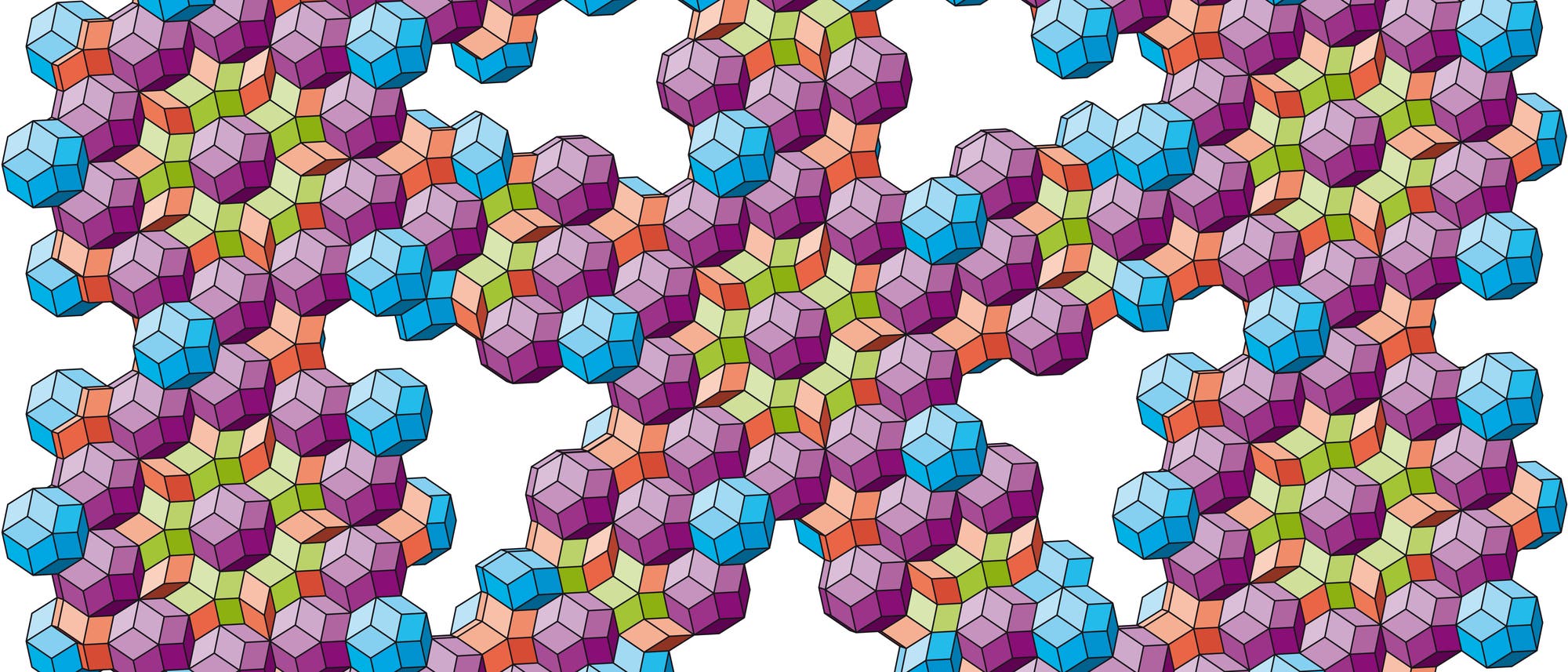
In der letzten Folge dieser Rubrik ging es darum, wie Künstler die speziellen Eigenschaften der so genannten Penrose-Parkette für ihre Zwecke nutzen. Deren Urbausteine sind zwei »goldene Dreiecke«: gleichschenklige Dreiecke mit dem Seitenverhältnis des goldenen Schnitts (τ ≈ 1,618), ein breites mit langer Basis und kurzen Schenkeln und ein hohes, bei dem die Schenkel τ-mal so lang sind wie die Basis. Zwei Exemplare eines goldenen Dreiecks, mit den Basen aneinandergelegt, ergeben eine dicke beziehungs- weise eine dünne Raute, und dies sind die Pflastersteine, mit denen man ein im Prinzip unendliches Parkett legen kann. Allerdings nicht beliebig! Spezielle »Anlegeregeln«, anschaulich gemacht durch eine Musterung der Steine oder eine Deformation ihrer Kanten, erzwingen, dass das Parkett nichtperiodisch ist. Das heißt, anders als in der klassischen Badezimmerkachelung gibt es keine Parallelverschiebung, die das ganze Parkett mit sich selbst zur Deckung bringt. Vielmehr steckt in dem ganzen Muster eine fünfzählige Symmetrie – irgendwie.

Ein sehr mächtiges theoretisches Hilfsmittel zum Verständnis der nichtperiodischen Parkettierungen ist die so genannte Substitution. Man zerlegt jeden Stein in eine Menge verkleinerter Exemplare aus demselben Steinsortiment und vergrößert das so erhaltene Parkettfragment so, dass jeder Stein wieder die Originalgröße hat. Diese beiden Schritte kann man beliebig oft wiederholen mit dem Effekt, dass ein beliebig kleiner Teil eines Parketts – ein einziger Stein genügt – schrittweise zu immer größeren Flächen heranwächst und im Grenzwert die ganze unendliche Ebene bedeckt.

Vom Standpunkt der Festkörperphysiker aus ist die ganze schöne Theorie der Penrose-Parkette nur eine Vorübung für dasselbe in drei statt zwei Dimensionen …