Wenn man einen Kreis zwischen zwei parallele Geraden einklemmt, dann ist der Abstand zwischen ihnen stets derselbe, einerlei wie der Kreis orientiert ist. Das wussten schon die ägyptischen Pyramidenbauer: Ein schwerer Steinquader lässt sich mit Hilfe kreisrunder Rollen über ebenen Untergrund transportieren, ohne sich auf und abzubewegen.

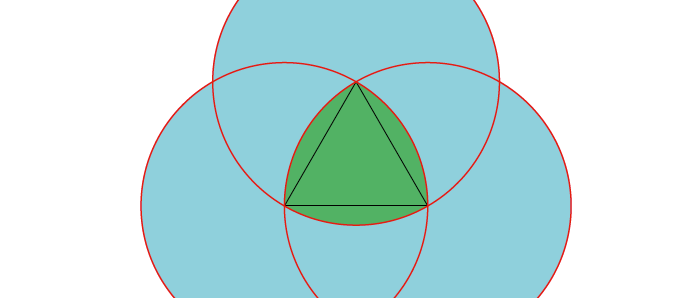
Gilt das auch umgekehrt? Wenn der Steinklotz nicht auf- und abschwankt, können wir dann sicher sein, dass die Rolle einen kreisförmigen Querschnitt hat? Eben nicht! An Stelle des Kreises tut es auch ein so genanntes Reuleaux- Dreieck. Es entsteht aus einem gleichseitigen Dreieck, indem man in jede seiner Ecken einen Zirkel einsticht und die beiden jeweils anderen Ecken durch einen Kreisbogen verbindet.

Die Mathematiker nennen den Abstand zweier paralleler, dicht an der Kurve anliegender Geraden eine "Dicke" dieser Kurve, obgleich man normalerweise eher von der Dicke (oder Breite) der Fläche sprechen würde, die von der Kurve eingeschlossen wird. Je nach der Orientierung der Geraden kann ein und dieselbe geschlossene Kurve unterschiedliche Dicken aufweisen. Wenn sie in jeder Richtung gleich dick ist, nennt man sie eine Kurve konstanter Dicke, kurz "Gleichdick-Kurve" oder auch "Gleichdick". Weitere Gleichdicke entstehen durch die entsprechende Konstruktion aus regelmäßigen Vielecken mit fünf, sieben oder allgemein einer beliebigen ungeraden Anzahl von Seiten ...