»Als ich erstmals von höherer Kategorientheorie gehört habe, habe ich die Nase gerümpft und gedacht: ›Was ist das denn für eine Spinnerei‹«, erinnert sich der Informatiker Thorsten Altenkirch von der University of Nottingham. »Wie sich herausstellt, ist es genau das, was man braucht.« Mit diesem Eindruck war er nicht allein: In ihren Anfängen fand die abstrakteste aller mathematischen Disziplinen, wie sie oft genannt wird, keinen großen Anklang. Häufig bezeichneten sie Fachleute – zum Teil auch humorvoll – als »abstrakten Unsinn«. Dass das Gebiet äußerst nützlich sein kann, ist inzwischen aber unumstritten.

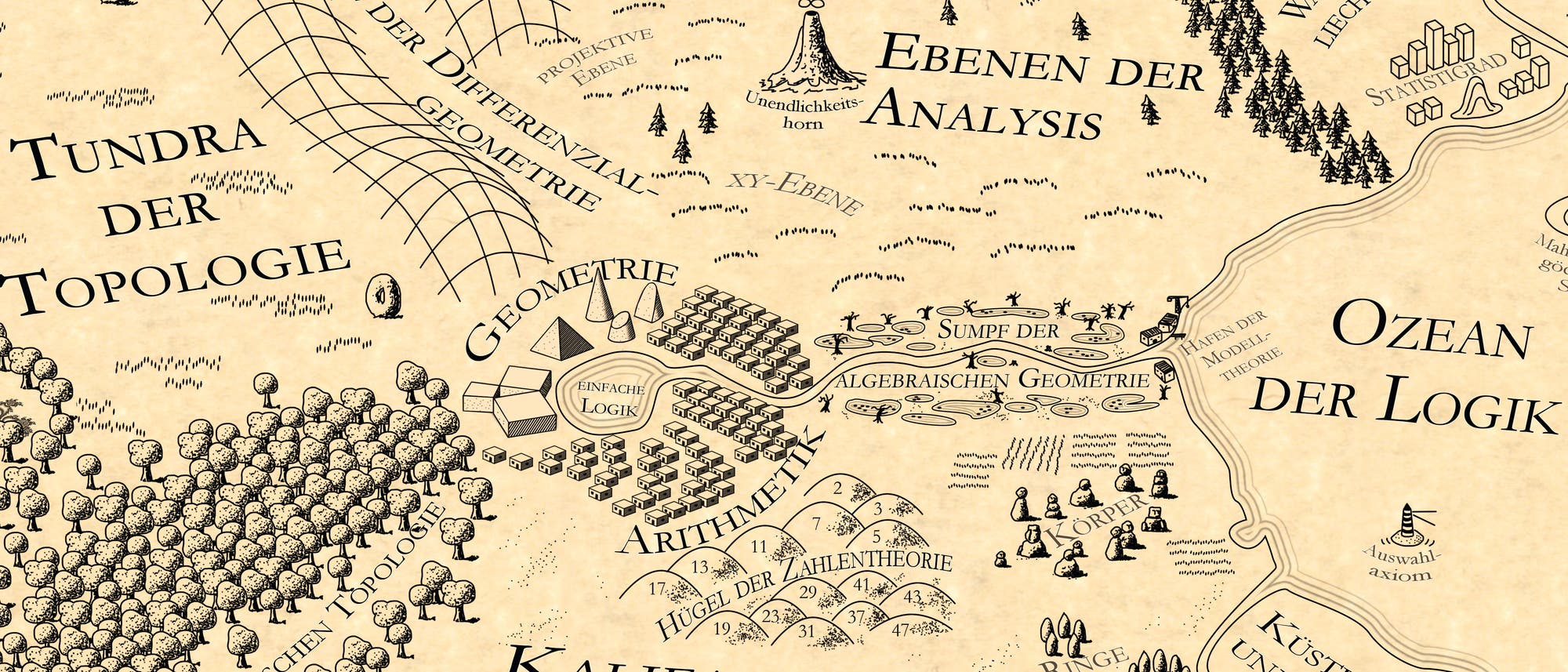
Man kann sich die Kategorientheorie als Vogelflug über die Welt der Mathematik vorstellen, wie es Martin Kuppe dargestellt hat: Aus dieser Vogelperspektive überblickt man die verschiedenen Bereiche des Fachs – ein Traum, den viele Fachleute hegen: Relativ mittig offenbart sich das bekannte Reich der Arithmetik, in dem Zahlen miteinander addiert, multipliziert, voneinander abgezogen und dividiert werden. Daran grenzen die Hügel der Zahlentheorie an, in der Primzahlen und andere seltsame Konstrukte lauern, während sich südlich das riesige Kalifat der Algebra erstreckt, in dem nicht nur mit Zahlen gerechnet wird, sondern auch mit komplizierteren Objekten wie Matrizen.

In dieser Schwindel erregenden Höhe verschwimmen die Details der einzelnen Gebiete, man kann bloß grobe Strukturen erkennen. Doch diese Ungenauigkeit ist einer der Vorteile der Kategorientheorie, der »Mathematik aus der Vogelperspektive«. Denn dafür werden größere Zusammenhänge plötzlich sichtbar: Es lassen sich Brücken und Grenzregionen zwischen den verschiedenen Reichen ausmachen. Beispielsweise liegen zwischen der Tundra der Topologie und dem Kalifat der Algebra die Wälder der algebraischen Topologie. Darin sind die Konzepte aus beiden Welten vereint: Während die Bewohner der Tundra geometrische Objekte nach der Anzahl ihrer Löcher ordnen, können algebraische Topologen die Löcher durch algebraische Konstrukte wie Funktionen oder Gruppen ausmachen.

Dass ein solches übergeordnetes mathematisches Konzept nötig ist, ist der zunehmenden Komplexität des Fachs geschuldet. Vor mehreren hundert Jahren gab es noch Universalgelehrte, die sich in fast allen Wissenschaften auskannten, von Philosophie über Physik bis hin zu Medizin. Ihre Erkenntnisse in einem Fachgebiet halfen ihnen in anderen Bereichen weiter. An so etwas ist heute nicht mehr zu denken. Eine Zahlentheoretikerin und ein Stochastiker werden einander höchstwahrscheinlich nur schwer verstehen – und das, obwohl beide Mathematiker sind.

»Mich hat dieser ›Aha-Moment‹ schon immer angezogen, der aufkommt, wenn sich scheinbar ungleiche Ideen vereinheitlichen lassen«Tai-Danae Bradley, Mathematikerin

Dabei sind die einzelnen mathematischen Disziplinen gar nicht so unterschiedlich, wie sie auf den ersten Blick scheinen. Tatsächlich decken Fachleute immer wieder Gemeinsamkeiten zwischen verschiedenen Bereichen auf. Wenn etwa ein Problem aus der Analysis, die sich häufig mit Funktionen beschäftigt, einer ungelösten Aufgabe aus der Zahlentheorie gleicht, lassen sich die Werkzeuge aus dem einen Gebiet auf das andere übertragen. Doch dazu muss man bereit sein, das eigene vertraute Reich zu verlassen und eine Vogelperspektive einzunehmen, um sich nicht in den Details der einen oder anderen Disziplin zu verlieren. Genau das versucht die Kategorientheorie zu erreichen.

»Mich hat dieser ›Aha-Moment‹ schon immer angezogen, der aufkommt, wenn sich scheinbar ungleiche Ideen vereinheitlichen lassen«, erzählt die Mathematikerin Tai-Danae Bradley von der City University of New York, die an der Kategorientheorie forscht. »Deshalb war ich sehr aufgeregt, als ich zum ersten Mal von einem Zweig der Mathematik erfuhr, der dabei hilft, klar über solche übergreifenden Konzepte nachzudenken.«

Ein derartiger Perspektivenwechsel hat aber auch Nachteile. Kategorientheoretiker schweben in so hohen Sphären, dass sie kaum explizite Ergebnisse liefern: Sie werden niemals eine Differenzialgleichung lösen oder ein Integral berechnen. Andererseits können sie unbekannte Wege entdecken, die zur Lösung eines handfesten Problems führen. Um diese tatsächlich zu berechnen, muss man dann jedoch wieder auf den Boden der Tatsachen zurückkehren und die Arbeit im passenden Gebiet erledigen.

Das ist wohl auch der Grund dafür, warum es mehrere Jahrzehnte dauerte, bis die Theorie in Gang kam. Zunächst nur als mathematisches Werkzeug in den 1940er Jahren entwickelt, führte das Konzept der Kategorien in den 50er und 60er Jahren zu bedeutenden Erkenntnissen, die gesamte Bereiche wie die algebraische Geometrie bis heute prägen. Viele mathematische Fortschritte der letzten 70 Jahre wären ohne die Kategorientheorie undenkbar. Doch selbst heute scheiden sich die Geister, ob es sich dabei wirklich um eine eigenständige Theorie handelt oder bloß um ein hilfreiches Begriffssystem, mit dem man komplizierte Sachverhalte einfacher darstellen kann.

Obwohl sie als der abstrakteste aller mathematischen Bereiche gilt, taucht die Kategorientheorie in den letzten Jahren vermehrt in anderen Wissenschaften auf, um deren Probleme in einem neuen Licht darzustellen. So greifen beispielsweise Informatiker darauf zurück, um neue Programmiersprachen zu entwickeln, Physikerinnen und Physiker untersuchen mit Kategorien exotische Materiezustände, und auch in der Linguistik werden mit dem abstrakten Konzept grammatikalische Gemeinsamkeiten verschiedener Sprachen aufgedeckt.

Auf die grobe Struktur kommt es an

Kategorien fügen sich so gut in verschiedenste Disziplinen ein, weil sie ganz allgemein definiert sind: Eine Kategorie besteht aus einer Sammlung von Dingen, die sich durch Morphismen (eine Art Abbildung) ineinander umwandeln lassen. Worum genau es sich bei den Dingen und Morphismen handelt, ist nicht entscheidend.

Ein Beispiel für eine Kategorie sind einzelne natürliche Zahlen (1, 2, 3, …), die als Objekte dienen, und Funktionen zwischen ihnen (f(n) = m) als Morphismen. Oder aber man betrachtet die gesamten natürlichen Zahlen als einziges Objekt und alle Funktionen, die natürliche Zahlen auf sich selbst abbilden, als Morphismen.

Bei Kategorien sind der Kreativität keine Grenzen gesetzt: Auch Oberflächen können Objekte darstellen, während die Transformationen, die sie ineinander umformen, den Morphismen entsprechen. Ganz allgemein kann man sich eine Kategorie als Sammlung von Pfeilen (Morphismen) vorstellen, die verschiedene Punkte (Objekte) miteinander verbindet. Was genau die Pfeile und die Punkte repräsentieren, spielt keine Rolle, entscheidend ist nur, wie sie zusammenhängen.

Ein Objekt ist vollständig durch seine Beziehung zu den anderen Dingen definiert – unabhängig davon, ob es sich dabei um eine Zahl, eine Oberfläche oder etwas Abstrakteres handelt

Diese Ansicht stellte vor 70 Jahren einen drastischen Paradigmenwechsel dar. Denn die Mengenlehre, ein Bereich, auf dem fast die gesamte Mathematik fußt, definiert die betreffenden Objekte sehr klar. In der Kategorientheorie erscheinen hingegen natürliche Zahlen und geometrische Formen manchmal ununterscheidbar, während die Kategorie der Zahlen, die durch stetige Funktionen verknüpft sind, völlig anders ist als die Kategorie der Zahlen gepaart mit differenzierbaren Funktionen. Ein Objekt ist also vollständig durch seine Beziehung zu den anderen Objekten definiert – unabhängig davon, ob es sich dabei um eine Zahl, eine Oberfläche oder etwas Abstrakteres handelt.

Das mag ungewöhnlich klingen, doch der Gedanke ist nicht neu: In der Physik identifiziert man zum Beispiel ein Teilchen in einem Beschleuniger, indem man es mit anderen Partikeln bombardiert und die Wechselwirkungen zwischen ihnen untersucht. Die Kategorientheorie bietet einen allgemeinen Rahmen, den Fachleute mit Objekten und Abbildungen ihres jeweiligen Bereichs füllen können. Sie müssen dabei nicht zwischen einzelnen Fachgebieten unterscheiden, sondern konzentrieren sich lediglich auf die jeweiligen zu Grunde liegenden Strukturen.

Kategorien von Kategorien offenbaren Zusammenhänge

Diese Idee kann man auf die Spitze treiben: Da es egal ist, mit welchen Objekten man eine Kategorie füllt, kann man sie auch ihrerseits mit Kategorien füllen, wodurch eine »höhere Kategorie« entsteht. Damit lassen sich Brücken zwischen mathematischen Disziplinen entdecken, denn diese entsprechen gerade den Umwandlungen, so genannten Funktoren, die eine Kategorie in eine andere überführen.

Eines der bekanntesten Beispiele für einen Funktor fand der französische Gelehrte René Descartes bereits im 17. Jahrhundert, lange bevor es die Kategorientheorie überhaupt gab. Damals stellte er fest, dass viele geometrische Probleme durch algebraische Gleichungen lösbar sind. Es gelang ihm, das nach ihm benannte kartesische Koordinatensystem einzuführen, womit er den ersten Zusammenhang zwischen der Geometrie und der Algebra begründete. Da sich beide Gebiete als Kategorien auffassen lassen, kann man einen Funktor finden, der beide ineinander umwandelt. Die Geometrie und die Algebra bilden damit eine höhere Kategorie.

Die Geburtsstunde der abstrakten Theorie ließ dann allerdings noch 300 Jahre auf sich warten. 1941 hielt der US-amerikanische Mathematiker Saunders Mac Lane an der University of Michigan eine sechsteilige Vortragsreihe über seine jüngsten Forschungsergebnisse im Bereich der Zahlentheorie. Im Publikum saß unter anderem sein Kollege Samuel Eilenberg, der am letzten Vortrag nicht teilnehmen konnte. Als er wenig später Mac Lane aufsuchte, wiederholte dieser die Präsentation in einem privaten Rahmen. Eilenberg traute seinen Augen kaum: Sein Kollege konstruierte dabei ein mathematisches Objekt, das er schon einmal in einem völlig anderen Zusammenhang gesehen hatte, nämlich im Bereich der Topologie.

Das erschien äußerst seltsam, schließlich haben Topologie und Zahlentheorie nur wenig gemeinsam: Während sich die Topologie mit dem Ordnen von geometrischen Figuren beschäftigt, widmen sich Zahlentheoretiker unterschiedlichen Zahlensystemen. Doch wie sich herausstellt, hängen beide Bereiche eng mit der Algebra zusammen, die gewissermaßen eine Brücke zwischen beide Gebiete schlägt. Um das zu verstehen, muss man ein wenig tiefer in die Disziplinen eintauchen.

Topologie schafft Ordnung unter den Formen

Die Topologie ist wie eine Art Geometrie, die das Messen von Längen verlernt hat. Sie beschreibt zwar auch geometrische Formen und Körper, die Details entgehen ihr jedoch. Sobald man zwei Objekte ineinander verformen kann, ohne Löcher in sie zu reißen, sind sie für Topologen identisch. Anders als bei der Geometrie dauerte es recht lange, bis Mathematiker und Mathematikerinnen bemerkten, dass sich topologische Konzepte auch in die Sprache der Algebra übertragen lassen.

Anfang des 20. Jahrhunderts steckte die algebraische Topologie noch in den Kinderschuhen. Der Grund dafür ist die Ungenauigkeit, welche die Topologie ausmacht. Eine quadratische Gleichung wie x² + y² = 1 beschreibt zum Beispiel einen Kreis. Eine Ellipse, die topologisch gesehen identisch ist, entspricht dagegen einer völlig anderen Gleichung.

Da Funktionen nicht weiterhalfen, wandten sich Fachleute anderen algebraischen Objekten zu: den ganzen Zahlen. Mit diesen lassen sich verschiedene Objekte klassifizieren, etwa geometrische Oberflächen, indem man die Anzahl ihrer Löcher zählt. Die Lochzahl wird als »topologische Invariante« bezeichnet, weil topologisch äquivalente Dinge immer die gleiche Lochzahl haben. Während ein Brötchen (null Löcher) und eine Brezel (drei Löcher) topologisch gesehen grundverschieden sind, erscheinen eine Tasse (ein Loch) und ein Donut (ein Loch) hier gleich.

Diese simple Klassifizierung ist leicht verständlich. Auf formaler Ebene kann sie sich aber recht schwierig gestalten. Muss man jede geometrische Form erst visualisieren, um auf die Anzahl ihrer Löcher und damit auf ihre topologischen Invarianten zu schließen? In zwei Dimensionen mag das ja möglich sein, doch sobald man sich mehrdimensionalen Problemen stellt, führt es zu Schwierigkeiten.

Daher suchten Fachleute nach einer Methode, Löcher mit algebraischen Mitteln aufzuspüren. Henri Poincaré erkannte 1895 als einer der Ersten, dass eine Möglichkeit darin besteht, alle möglichen geschlossenen Kurven auf einer geometrischen Form zu untersuchen. Wenn sich jede Kurve – ohne die Oberfläche zu durchdringen oder zu verlassen – wie ein Lasso zusammenziehen lässt, dann gibt es kein Loch. Das ist auf einer Kugel der Fall. Bei einem Torus, einer donutförmigen Oberfläche, gibt es dagegen gleich zwei verschiedene Arten von Kurven, die man nicht zusammenziehen kann.

Allerdings sind die Objekte der Topologie-Kategorie, so genannte topologische Räume, nicht immer so anschaulich wie eine Kugel oder ein Torus. Sie können unzusammenhängende Formen in Schwindel erregend hohen Dimensionen sein oder aus Elementen seltsamer Zahlensysteme bestehen. In solchen Fällen sind sie nicht so einfach zu klassifizieren.

Wie beschreibt man Löcher durch Algebra?

Als sich die deutsche Mathematikerin Emmy Noether Anfang des 20. Jahrhunderts mit diesen Problemen beschäftigte, fiel ihr auf, dass topologische Räume nicht nur mit ganzen Zahlen, sondern auch mit so genannten Gruppen zusammenhängen. Die einfachsten Versionen dieser Objekte bestehen aus Symmetrietransformationen wie Drehungen oder Spiegelungen. Beispielsweise lässt sich ein gleichseitiges Dreieck entlang von drei Achsen spiegeln und um 0, 120 oder 240 Grad drehen, ohne dass es sein Aussehen verändert. Diese sechs Transformationen entsprechen daher der Symmetriegruppe des Dreiecks. Im Allgemeinen ähnelt die Definition einer Gruppe der einer Kategorie: Sie ist eine Sammlung von Dingen, die man aufeinander abbilden kann, und besitzt ebenfalls ein neutrales Element. Eine Gruppe jedoch muss eine weitere Anforderung erfüllen: Zu jedem Element gibt es ein »Inverses«, so dass beide miteinander verknüpft das neutrale Element ergeben.

Wie Noether herausfand, gibt es eine bestimmte Art von Gruppen, so genannte Homologiegruppen, aus denen sich topologische Invarianten wie die Lochzahl berechnen lassen. Verformt man ein geometrisches Objekt, ohne dabei die dazugehörigen Invarianten zu verändern, gibt es ganz ähnliche Transformationen, die Homologiegruppen ineinander umwandeln, wobei auch ihre topologischen Invarianten gleich bleiben. Scheitert man also an der Aufgabe, die Invariante eines topologischen Raums zu berechnen, kann man sich stattdessen den dazugehörigen Homologiegruppen zuwenden.

Damit begründete die deutsche Mathematikerin eine neue Ära der algebraischen Topologie. Plötzlich standen nicht mehr nur die topologischen Räume im Rampenlicht, sondern auch die Beziehungen zwischen ihnen. Denn die Transformationen, die einen Raum verformen, ohne Löcher in ihn zu reißen, hängen mit den Abbildungen zwischen den dazugehörigen Homologiegruppen zusammen. Damit zeichnete sich damals schon das Hauptmerkmal der Kategorientheorie ab, dessen Fokus auf den Zusammenhängen zwischen Objekten liegt.

Diesen Homologiegruppen hatte sich Eilenberg gewidmet, bevor er an die University of Michigan gereist war. Und genau so ein Objekt hatte er in Mac Lanes Vortrag erkannt – und war äußerst überrascht.

Gruppen in der Zahlentheorie

Denn Mac Lane untersuchte eigentlich völlig andere Gruppen, die in der Zahlentheorie auftauchen. Verknüpft man Zahlen miteinander, lässt sich dabei häufig eine Gruppenstruktur erkennen. So bilden etwa die ganzen Zahlen zusammen mit der Addition eine Gruppe: Zwei ganze Zahlen a und b ergeben verknüpft wieder eine ganze Zahl a + b = c, 0 ist das neutrale Element und jede ganze Zahl a hat ein Inverses −a. Gerade in den abstrakten Bereichen der Zahlentheorie ist es häufig nützlich, statt der Zahlen selbst die dazugehörigen Gruppen zu studieren.

Mac Lane interessierte sich damals für extrem komplizierte Zahlensysteme. Um seine Berechnungen zu vereinfachen, verfrachtete er das Problem daher in den Bereich der Algebra. Dazu konstruierte er eine spezielle Art von Gruppe, eine so genannte Erweiterung von Gruppen. Einfach ausgedrückt besteht ein solches Objekt aus einer Gruppe G, die um eine andere Gruppe H »vergrößert« wird, so dass daraus wieder eine Gruppe entsteht.

»Wir blieben die ganze Nacht auf, um herauszufinden, warum das so war«Saunders Mac Lane, Mathematiker

Eilenberg erkannte die Gruppenerweiterung von Mac Lane sofort wieder. Er hatte sie bereits in der Arbeit seines Kollegen Norman Steenrod gesehen, in der dieser einen komplizierten topologischen Raum untersucht hatte. Der Raum ergibt sich, wenn man einen Torus (die Oberfläche eines Donuts) nimmt und in dessen Inneren einen weiteren Torus p-mal hineinwickelt, in diesen wieder einen Torus p-mal hineinwickelt und das Ganze unendlich oft wiederholt. Die Schnittmenge all dieser Tori ergibt den topologischen Raum, dessen dazugehörige Homologiegruppe der Gruppe von Mac Lane entsprach.

»Wir blieben die ganze Nacht auf, um herauszufinden, warum das so war«, erinnerte sich Mac Lane. Das war der Beginn einer fruchtbaren Zusammenarbeit und einer lebenslangen Freundschaft zwischen den beiden Forschern.

Die Verbindung vereinfacht die Berechnungen

Was die beiden so faszinierte, war, dass die Berechnungen von Mac Lane wesentlich einfacher ausfielen als jene im Zusammenhang mit topologischen Räumen. Häufig ist es nämlich extrem schwierig, Homologiegruppen zu berechnen. Doch wie die Mathematiker nach einigen Monaten herausfanden, bilden die Erweiterungen von Gruppen eine Art Brücke zwischen verschiedenen algebraischen Methoden, die topologische Eigenschaften eines Raums offenlegen. Das war ein echter Durchbruch. Wenn ein algebraischer Ansatz nicht funktionierte, konnten die Erweiterungen von Gruppen einen anderen Weg aufzeigen, um einen topologischen Raum zu untersuchen.

»Da war mehr, als wir erwartet hatten. Wir waren gezwungen, Kategorien zu erfinden, um das zu beschreiben«Saunders Mac Lane, Mathematiker

In den kommenden Jahren fanden die zwei Forscher weitere Übereinstimmungen zwischen der Algebra und der Topologie. »Da war mehr, als wir erwartet hatten«, sagte Mac Lane. »Wir waren gezwungen, Kategorien zu erfinden, um das zu beschreiben.« Sie definierten Kategorien damals allerdings nicht als die abstrakten Objekte, die man heute kennt, sondern betrachteten bloß den Spezialfall einer Kategorie, die aus Gruppen besteht. Kategorien dienten ihnen als Werkzeug.

Wissenschaftler schenkten den neu eingeführten Kategorien damals kaum Beachtung. Erst Alexander Grothendieck erkannte, wie nützlich das abstrakte Konzept wirklich sein kann. Der Mathematiker zählt zu den einflussreichsten und bedeutendsten Meistern seines Fachs – zumindest bis er sich 1991 in ein kleines französisches Bergdorf zurückzog und jeglichen Kontakt zur Außenwelt abbrach.

Ein Außenseiter krempelt das Fach um

Bis kurz nach seiner Promotion hatte sich Grothendieck der Analysis gewidmet, bei der es hauptsächlich darum geht, geometrische Objekte mit differenzierbaren Funktionen zu vermessen. Sein Forschungsinteresse wandelte sich allerdings schlagartig, als er Mitte der 1950er Jahre in die USA auswanderte. Zuvor hatte er keine Anstellung in Frankreich gefunden, weil er sich weigerte, die französische Staatsbürgerschaft anzunehmen, um dem Militärdienst zu entgehen – und war daher mehrere Jahre staatenlos.

Während eines Forschungsaufenthalts in Kansas begann er, sich mit algebraischer Topologie auseinanderzusetzen. Damals war das Gebiet noch ziemlich chaotisch. Tatsächlich sucht man noch heute nach einem allgemeinen Rezept, das für jede Art von topologischem Raum die dazugehörige Homologiegruppe ausspuckt. Bisher gibt es zwar mehrere Methoden, so genannte Homologien, die sich aber je nach Art des Raums voneinander unterscheiden. Grothendieck gelang es mit Hilfe der Kategorientheorie, ein gemeinsames Fundament für viele dieser Konzepte zu schaffen. Auf diese Weise entdeckte er weitere Homologien, mit denen sich die Homologiegruppen eines topologischen Raums berechnen lassen.

Damals interessierte sich Grothendieck vor allem für so genannte Garben, die auf komplizierten topologischen Räumen auftauchen. Formal sind topologische Räume als Vereinigung von Mengen definiert – man »klebt« einzelne Bereiche zusammen. Wenn man ein algebraisches Objekt wie eine Funktion auf einem solchen Raum betrachtet, muss man verstehen, wie es sich an den Klebestellen verhält. Dabei hilft die Theorie der Garben.

Die Garbentheorie arbeitet meist lokal: Man arbeitet sich von Punkt zu Punkt in einem Raum fort, ohne die globale Struktur zu beachten. Beispielsweise macht es keinen Unterschied, ob man die Funktionen auf einer zylinderförmigen Fläche zusammenklebt oder auf einem Möbiusband. Bei der Topologie sind jedoch hauptsächlich die globalen Eigenschaften eines Raums ausschlaggebend – Möbiusband und Zylinder sind zwei grundsätzlich verschiedene Objekte. Daher suchten viele Mathematiker Mitte der 1950er Jahre nach einer homologischen Theorie der Garben, die erklären würde, wie die globalen Merkmale eines Raums mit den darauf definierten algebraischen Objekten zusammenhängen.

Grothendieck behandelte Kategorien erstmals nicht nur als Werkzeug, sondern als eigenständige Theorie

Auch Eilenberg wusste, dass es eine homologische Theorie der Garben geben musste. Doch weder ihm noch seinen Kollegen gelang es, eine solche zu konstruieren. Erst Grothendieck fand eine Lösung, indem er einen Umweg ging und sich zunächst Kategorien zuwendete. Im Gegensatz zu seinen Kollegen Mac Lane und Eilenberg, die Kategorien nutzten, um ein bestimmtes Problem anzugehen, strebte Grothendieck nach Höherem. Er suchte nach einem übergreifenden Rahmen, der Homologien erweitert. Dabei behandelte er Kategorien erstmals nicht nur als Werkzeug, sondern als eigenständige Theorie, die verschiedene Bereiche miteinander verschmilzt. So konnte er Verbindungen zwischen Verbindungen erkennen: Plötzlich verstand er, wie einige Homologien zusammenhängen – er hatte Abbildungen gefunden, die Homologien auf andere Homologien abbilden. Dadurch war er in der Lage, völlig neue Homologien zu entwickeln, darunter eine für Garben.

Die Verschmelzung von Algebra und Geometrie

Nach diesen bahnbrechenden Entdeckungen wandte sich Grothendieck einem neuen Bereich zu, der algebraischen Geometrie. Und auch hier vermochte er das Gebiet mit Hilfe von Kategorien zu revolutionieren. Die algebraische Geometrie behandelt geometrische Formen, die sich aus Gleichungen von Polynomen (etwa 3x⁴y² + 2x + 6y² + 5 = 0) ergeben.

Grothendieck beförderte die algebraische Geometrie auf eine abstraktere Stufe, indem er nicht bloß Polynome als Forschungsgegenstände zuließ, sondern allgemeinere algebraische Strukturen, so genannte Ringe. Diese ähneln Gruppen, nur dass sie zwei Verknüpfungen zwischen ihren Elementen enthalten. Ein Beispiel für Ringe sind die rationalen Zahlen, die man addieren und multiplizieren kann. Da sich auch Polynome addieren und miteinander multiplizieren lassen, bilden sie ebenfalls einen Ring.

Frei nach dem Prinzip der Kategorientheorie ließ Grothendieck spezielle Objekte (Polynome) los und ersetzte sie durch allgemeinere Strukturen (Ringe). So offenbarte der Mathematiker unerwartete Zusammenhänge zwischen der algebraischen Geometrie und anderen mathematischen Disziplinen wie der Zahlentheorie. Man kann sich kaum vorstellen, wie diese Bereiche ohne Grothendiecks Zutun aussehen würden.

Die Kategorientheorie als neues Fundament der Mathematik

Nach diesen und vielen anderen beeindruckenden Ergebnissen wurde die Kategorientheorie immer beliebter. Der US-amerikanische Forscher William Lawvere ging in seiner Doktorarbeit 1963 sogar noch einen Schritt weiter: Er äußerte die Idee, die gesamte Mathematik auf der Kategorientheorie zu begründen und damit die Mengenlehre als Grundlage abzulösen. Ihm und vielen seiner Kollegen gefiel der Gedanke eines übergreifenden Rahmens, bei dem nicht die genaue Art der Objekte entscheidend ist, sondern ihre Verbindungen zueinander. »Viele Mathematiker haben eine kategorische Denkweise, selbst wenn sie nicht alle Konzepte oder Theoreme nutzen«, meint Tai-Danae Bradley.

Anstatt also die Mathematik aus den Axiomen der Zermelo-Fraenkel-Mengenlehre aufzubauen, die die moderne Grundlage des Fachs bilden, schlug Lawvere vor, Mengen durch Kategorien zu definieren und daraus alles herzuleiten. Allerdings interessierten sich nur wenige Mathematiker für diesen Ansatz. »Wissenschaftler widmen ihre Zeit interessanteren Dingen«, erklärt Steve Awodey von der Carnegie Mellon University in Pittsburgh.

Aus einigen Konzepten der Kategorientheorie ging die Homotopietypentheorie (HoTT) hervor, die der 2017 verstorbene russische Mathematiker Vladimir Voevodsky zusammen mit Awodey und anderen mitbegründet hat. »Dafür muss man zwar auch die Grundlage der Mathematik zumindest umschreiben, jedoch nicht aus philosophischen Gründen, sondern aus praktischen«, sagt Awodey. Ziel dieser Theorie ist es, Computern mathematische Formalismen wie Beweise zugänglich zu machen, um sie einfacher und schneller zu überprüfen.

Nützliches Tool oder abstrakter Unsinn?

Inzwischen zweifelt niemand mehr daran, dass die Kategorientheorie nützlich ist. Ohne sie gäbe es keine algebraische Geometrie oder algebraische Topologie – zumindest nicht in der Form, wie wir sie kennen. Dennoch sehen einige Forscher den Bereich nicht als eigenständige Theorie an. »Es ist nicht so, als schwebe die Kategorientheorie frei im Raum, vielmehr ist sie immer an andere Disziplinen gebunden. Deswegen ist sie für mich eher ein Begriffssystem«, meint Christoph Schweigert von der Universität Hamburg. Denn die besondere Kraft der Kategorientheorie bestehe darin, nützliche Verbindungen aufzudecken, die sich dann mit den Werkzeugen anderer mathematischer Disziplinen wie der Algebra oder Topologie auf konkrete Situationen anwenden lassen.

Andere Forscherinnen und Forscher teilen diese Ansicht allerdings nicht. »Es existieren auch eigenständige Zweige der Kategorientheorie. Es gibt viele Mathematiker, die Kategorientheoretiker sind, es gibt Tagungen zu diesem Thema, Zeitschriften, unzählige Veröffentlichungen und so weiter«, entgegnet Awodey.

Offenbar führt die Kategorientheorie noch heute zu Unstimmigkeiten. Gerade wenn es darum geht, was genau Äquivalenz bedeutet, liefert die abstrakte Theorie beispielsweise ganz andere Antworten als die Mengenlehre. Aus mengentheoretischer Sicht ist es einfach zu beurteilen, ob zwei Dinge identisch sind, da Objekte klar definiert sind. In der Kategorientheorie ist das anders. So etwas wie »die« natürlichen Zahlen gibt es nicht, sondern bloß »das Konzept der« natürlichen Zahlen. Daher sind aus kategorischer Sicht zwei Dinge gleich, wenn sie »isomorph« sind, das heißt, wenn es eine Abbildung und entsprechende Umkehrung gibt, die beide Objekte verbindet. Dieser Aspekt führte im 2018 zu einem Streit zwischen drei berühmten Mathematikern um einen vermeintlichen Beweis der ABC-Vermutung.

Anwendungen in verschiedenen Bereichen

Unterdessen betreiben einige Fachleute große Anstrengungen, die Kategorientheorie auch auf Probleme anderer Fachbereiche anzuwenden. Sie könnte Forschern dabei helfen, komplexe Systeme wie Schaltkreise oder chemische Reaktionen besser zu verstehen. John Carlos Baez von der University of California in Riverside organisierte in den vergangenen drei Jahren mehrere Konferenzen zu angewandter Kategorientheorie, um zu zeigen, dass die abstrakte Theorie auch in der Physik, Informatik, Linguistik, Biologie und vielen anderen Bereichen nützlich sein kann.

Festkörperphysiker bedienen sich der Kategorientheorie unter anderem, um exotische Zustände – so genannte topologische Phasen – von Materie zu beschreiben. In der Informatik werden die abstrakten Konzepte dagegen genutzt, um neue Programmiersprachen zu entwickeln, die weniger fehleranfällig sein sollen, ein Beispiel dafür ist »Haskell«. Einige Biologen und Biologinnen beschreiben hingegen, wie Enzyme in metabolischen Systemen ausgewechselt und repariert werden, indem sie auf Prinzipien der Kategorientheorie zurückgreifen. Ein weiteres Anwendungsbeispiel sind komplizierte chemische Reaktionen zwischen verschiedenen Molekülen. Und sogar für die Linguistik, die grammatikalische Gemeinsamkeiten verschiedener Sprachen behandelt, erweist sich das mathematische Gebiet als nützlich.

»Kategorientheorie kann man entweder lernen oder neu erfinden«Thorsten Altenkirch, Informatiker

Zudem kann die Kategorientheorie Fachleute unterschiedlicher Disziplinen zusammenführen. In der Vergangenheit hat sie Personen aus der Algebra und der Topologie nähergebracht, nun könnte sie das auch über die Fachbereiche hinaus tun, wie es der Mathematiker Schweigert auf einer Konferenz erlebte: »Es ist erstaunlich, plötzlich konnte ich mich mit einem Informatiker am Frühstückstisch darüber unterhalten, woran er gerade forscht – und wir benutzten eine gemeinsame Sprache!«

Dafür müssen Fachleute allerdings erst einmal bereit sein, einen ihnen gegebenenfalls unbekannten und abstrakten Formalismus zu lernen. Doch das kann sich lohnen; in einigen Bereichen der Informatik ist die abstrakte Theorie mittlerweile unerlässlich. »Kategorientheorie kann man entweder lernen oder neu erfinden«, erklärt Altenkirch. Auftauchen wird sie so oder so.