Eigentlich hatten Professor Chris Regan und sein Student Matthew Mecklenburg ganz anderes im Sinn: An der University of California in Los Angeles machten sie sich daran, bessere Transistoren, elektronische Halbleiterbauelemente, zu entwickeln. Zu ihrer Überraschung fanden sie sich inmitten grundlegender Gedanken zur Struktur des uns umgebenden dreidimensionalen Raums wieder. Sollte der Raum nicht unendlich oft teilbar sein? Schließlich gibt es doch zwischen zwei gegebenen Positionen immer eine Mitte, wo sich der Raum teilen ließe. Diese intuitive Vorstellung stürzen Regan und Mecklenburg nun um. Sie vermuten, dass der Raum auf kleinster Längenskala nicht glatt, sondern in diskrete Abschnitte unterteilt ist – ähnlich wie ein Schachbrett.

Zunächst untersuchten Regan und Mecklenburg die elektronischen Eigenschaften von Graphen, denn aus diesem neuartigen Material wollen ihre Kollegen einen Transistor bauen. Graphen besteht aus einer einzelnen Graphitschicht, ist also gerade so dick wie ein Atom. Die Kohlenstoffatome ordnen sich in einer wabenförmigen Struktur an. Das zweidimensionale Material besticht mit hoher elektrischer Leitfähigkeit und einer hohen Beweglichkeit der Elektronen. Wegen dieser ausgezeichneten elektronischen Eigenschaften zog es die Aufmerksamkeit der Technologen auf sich, die in ihm ein mögliches zukünftiges Transistormaterial sehen.

Wenn auf Graphen Schach gespielt wird

Die Elektronen der Kohlenstoffatome in Graphen bewegen sich, indem sie von einem Atom zum nächsten hüpfen. Obwohl Elektronen punktförmige Teilchen ohne räumliche Ausdehnung sind, tragen sie dennoch einen intrinsischen Drehimpuls in sich, den so genannten Spin. Dieser besitzt die quantenmechanische Eigenschaft, dass er nur in zwei Richtungen weisen kann: entweder aufwärts (Spin up) oder abwärts (Spin down). Die diskrete Natur des Spins erklärt die Stabilität der Materie, die chemischen Bindungen und andere fundamentale Phänomene.

Trotzdem ist noch unklar, wie das Elektron die von seinem Spin verursachte Rotationsbewegung ausführen kann. Hätte es eine räumliche Ausdehnung, so müsste sich seine Oberfläche schneller als die Lichtgeschwindigkeit drehen. Zum einen verletzte dies die Relativitätstheorie und zum anderen zeigten Experimente, dass das Elektron sich wie ein reines Punktteilchen verhält und keine Oberfläche oder Substruktur vorhanden ist, die rotieren könnte.

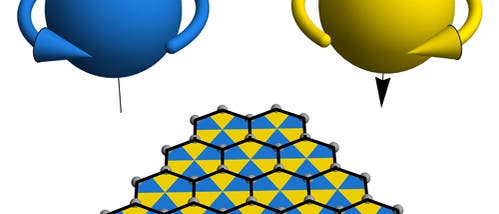
Regan und Mecklenburg fanden nun aber heraus, dass Teilchen einen Spin erhalten, wenn sie in einem Raum leben, der aus zwei verschiedenen Arten von Positionen besteht – so, wie das Schachbrett mit seinen schwarzen und weißen quadratischen Feldern. In der zweidimensionalen Graphenlandschaft sind die entsprechenden diskreten Flecken dreieckig, wobei die blauen Dreiecke aufwärts und die gelben entgegengesetzt abwärts zeigen (siehe beigestelltes Bild). Absorbiert ein Elektron Licht und damit Energie, so hüpft es einer Schachfigur gleich von einem blauen auf ein gelbes Dreieck. Dieser Übergang entspricht gleichzeitig einer Rotation des Spins: Aus "Spin up" wird "Spin down".

Wenn die Bewegung der Elektronen in Graphen also auf spezifische, diskrete Positionen eingegrenzt wird, so taucht ein Spin auf. Dieser entsteht durch die spezielle Bienenwabenstruktur von Graphen und ist vom gewöhnlichen quantenmechanischen Spin, den jedes einzelne Elektron trägt, zu unterscheiden. In Graphen widerspiegelt der zusätzliche Drehimpuls die schachbrettartige Struktur des Raums und gibt an, ob das Elektron ein blaues oder gelbes Dreieck besetzt. Dass sich aus dem Gitter aus Kohlenstoffatomen ein Spin erzeugen lässt, veranlasst die Wissenschaftler zu rätseln, ob der gewöhnliche Elektronenspin auf ähnliche Weise entsteht.

Rahel Heule