Form folgt Funktion: Dieser Leitsatz stammt eigentlich aus dem Design. Doch nun hat ihn eine Forschungsgruppe auch auf mathematische Funktionen übertragen. Nach einer speziellen Bauanleitung lassen sich jetzt physikalische Formen finden, die einen festgelegten Pfad beschreiten – so wie ein Zylinder eine schiefe Ebene immer entlang einer Geraden herunterrollt. Mit dem Algorithmus des Teams um Yaroslav I. Sobolev von der Universität Ulsan in Südkorea lässt sich ein Objekt finden, das einer beliebigen Kurve folgt. Diese kann von wilden Zacken durchsetzt sein wie bei einem EKG oder aus sanften Wellen bestehen wie eine Wasseroberfläche. »Unsere Arbeit ist vor allem durch grundlegende Neugier motiviert«, erklären die Forscher in ihrem Fachaufsatz, der im August 2023 bei »Nature« erschienen ist. Auch wenn es den Physikern sicherlich Freude bereitet hat, die vorhergesagten Formen mit einem 3-D-Drucker auszudrucken und schiefe Ebenen hinunterrollen zu lassen, ermöglicht die Arbeit zudem viele nützliche Anwendungen. So könnten die Erkenntnisse dabei helfen, wendige Roboter zu designen, Quantencomputer zu entwickeln oder medizinische Bildgebungsverfahren zu verbessern.

Lässt man einen Zylinder oder eine Kugel eine schiefe Ebene hinunterrollen, ist das Ergebnis nicht besonders spannend. Ohne weitere äußere Einwirkung folgen sie einer geraden Linie. Schon seit einigen Jahrzehnten sind Körper bekannt, die in dieser Hinsicht interessanter sind. So folgen ein »Oloid« oder ein »Sphericon« einer sinusartigen Kurve, die Formen wackeln also auf ihrem Weg in die Tiefe entlang einer glatten Kurve hin und her. »Hier endet jedoch schon die Vielfalt«, schreiben Sobolev und seine Kollegen in ihrer Veröffentlichung. Daher widmeten sich die Forscher der Frage, ob sich stets eine Figur finden lässt, die einem vorgegebenen Pfad folgt, wenn man sie eine schiefe Ebene herunterrollt.

Möchte man, dass die Figur bloß einem endlichen Weg folgt, lässt sich das einfach umsetzen. Man muss lediglich den gewünschten Pfad auf eine schiefe Ebene zeichnen und eine runde Kugel aus Knetmasse formen. Um die gewünschte Figur zu finden, übt man Druck auf die Knetmasse aus, während man sie entlang des Pfads rollt. Auf diese Weise entsteht eine Form, die Sobolev und seine Kollegen »Trajektoid« nennen. Sie nimmt automatisch den gewünschten Weg. Je größer die Oberfläche der Kugel ist, desto länger kann der Pfad sein, den sie entlangrollen soll. Trotzdem sind dem Ansatz Grenzen gesetzt: Eine Kugel hat bloß eine begrenzte Oberfläche, weshalb man auf diese Weise nur Pfade endlicher Länge in die Knetmasse »einprogrammieren« kann. Sobolev und seine Kollegen interessierten sich aber für unendlich lange periodische Pfade – also solche, die sich aus aneinandergereihten identischen Kurvenstücken zusammensetzen.

Um herauszufinden, für welche sich wiederholenden Pfade ein Trajektoid existiert, mussten die Forscher das Problem aus mathematischer Sicht beleuchten. Damit die Kugel einem periodischen Weg folgt, muss es entlang des Pfads einen Punkt P geben, ab dem sie ihre Bewegung wiederholt. Dafür braucht sie sowohl zum Ausgangspunkt A, an dem man die Kugel auf der schiefen Ebene absetzt, als auch bezüglich P exakt dieselbe Position. Nicht nur muss ihr Auflagepunkt der gleiche sein, sondern sie muss ebenso gleich ausgerichtet sein. Das lässt sich veranschaulichen, wenn man sich vorstellt, dass die Kugel bedruckt ist – zum Beispiel ein Globus. Blickt man jeweils an Punkt A und Punkt P frontal auf den Globus, sollte genau derselbe Ausschnitt der Weltkarte sichtbar sein.

Sobolev und seine Kollegen mussten also ermitteln, welche Eigenschaften eine Kurve zwischen zwei Punkten A und P erfüllen muss, damit eine Kugel, die entlang dieser Bahn rollt, am Anfang und Ende der Bewegung gleich ausgerichtet ist. Dafür stellten sie sich vor, die Kurve zwischen A und P sei ein dünner Draht, den man auf die Kugel legt. Da bei einer periodischen Bewegung der Kontaktpunkt der Kugel mit dem Boden am Start- und Endort gleich ist, muss der Draht eine geschlossene Kurve auf der Kugel bilden. Doch das alleine genügt nicht als Bedingung, damit die Form dem Pfad auch nach einer weiteren Umdrehung periodisch folgt. Sie könnte anschließend auch einen anderen Weg einschlagen.

Zwei Bedingungen an periodische Pfade

Hierfür haben sich Sobolev und seine Kollegen die Krümmung des vorgegebenen Pfads angesehen. Er muss einen bestimmten Verlauf haben, damit die Kugel am Ende des Wegs gleich ausgerichtet ist und sich somit periodisch bewegt. Stellen Sie sich einen Pfeil vor, der an jedem Ort senkrecht zum Verlauf der Kurve ausgerichtet ist und dessen Länge mit der Krümmung zusammenhängt – je stärker die Krümmung, desto länger der Pfeil. Folgt man dem Pfeil (ein so genannter Vektor) entlang des vorgegebenen Pfads, variiert sowohl seine Ausrichtung als auch seine Länge. Doch am Ende einer Periode muss der Pfeil genauso ausgerichtet und lang sein wie am Startpunkt. Der Krümmungsvektor ist also an Punkt A und P gleich.

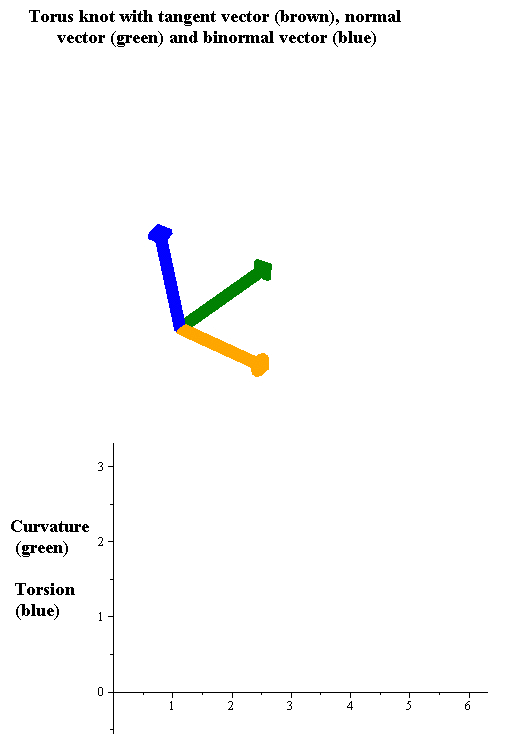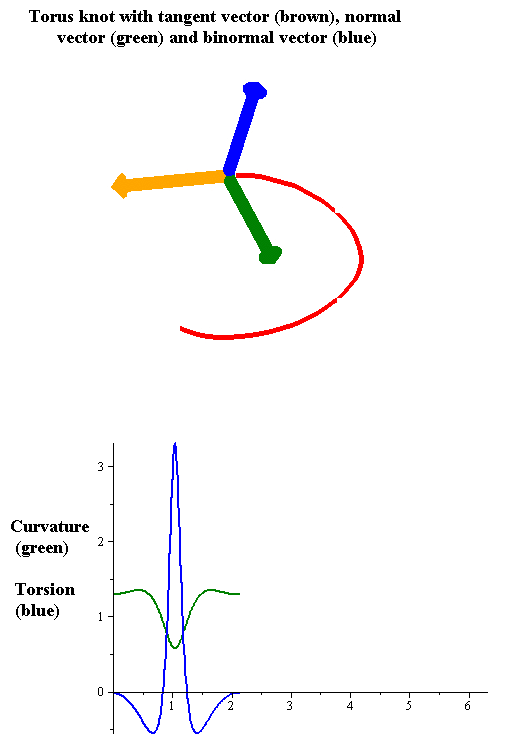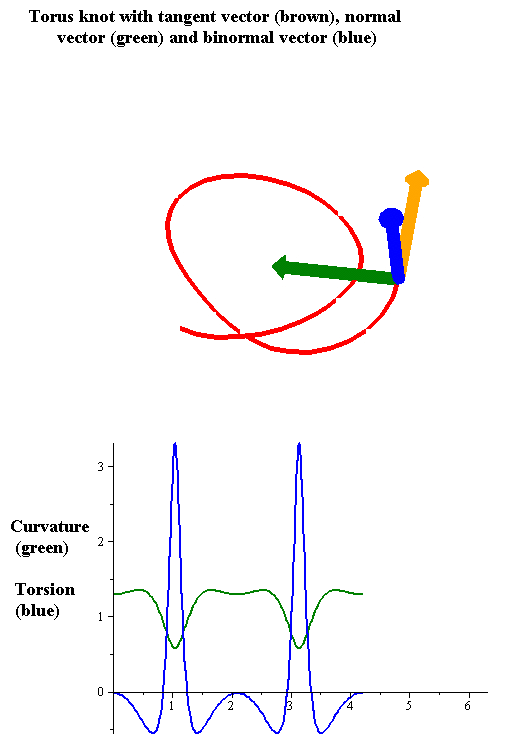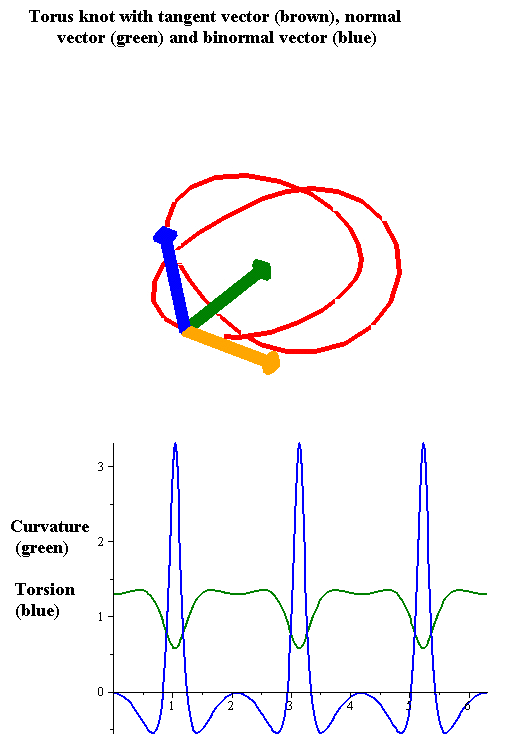
Diese Bedingung muss nicht nur auf der schiefen Ebene erfüllt sein, wo der Pfad eingezeichnet ist. Sie muss außerdem auf der Kugeloberfläche gelten: Auch dort muss die Krümmung des Drahts an Start- und Endpunkt gleich sein. Da eine Kugeloberfläche gewölbt ist, muss man hierbei nicht nur die Ausrichtung des Krümmungsvektors in der xy-Ebene beachten, sondern zusätzlich in der dritten Raumrichtung. Falls das Drahtstück nur einen kleinen Teil – oder einen zu großen Teil – der Kugeloberfläche einschließt, dann passt der Krümmungsvektor an den Endpunkten des Drahts nicht zusammen. Es entsteht ein Winkel zwischen beiden Pfeilen, so dass sie in verschiedene Richtungen zeigen.

Der Winkel α entsteht durch die Krümmung der Kugel. Und er führt dazu, dass die Kugel nach einem Umlauf entlang des Pfads einem anderen Weg folgt. In diesem Fall ist keine periodische Bewegung möglich. Falls die vom Draht eingeschlossene Fläche hingegen genau der halben Kugeloberfläche entspricht, passen die Krümmungsvektoren bei Start- und Endpunkt nahtlos zusammen. Der Winkel α schrumpft zu null. Um also ein Trajektoid zu einem vorgegebenen periodischen Pfad zu konstruieren, muss der Pfad zwei Bedingungen erfüllen: Auf eine Kugel aufgewickelt muss er eine geschlossene Kurve bilden, die genau die Hälfte ihrer Oberfläche einschließt.

Betrachtet man eine einzelne Periode eines Pfads, ist es unwahrscheinlich, dass der Abschnitt diese beiden Bedingungen erfüllt. Doch Sobolev und seine Kollegen machten eine interessante Entdeckung: Wenn man nicht bloß den ersten Abschnitt einer Periode betrachtet, sondern zwei, dann erfüllen die meisten Pfade die obigen Bedingungen. Das bedeutet, die Kugel landet nach dem Losrollen erst wieder in ihrer Ausgangsposition, nachdem sie zwei gleichen Teilen des Pfads gefolgt ist. Man müsste mit einer Kugel zum Beispiel einer Sinuskurve über eine Distanz von 4π folgen, bevor sie wieder ihre Anfangsposition einnimmt.

Die Physiker konnten einen Algorithmus entwickeln, der für zwei Perioden eines quasi beliebigen periodischen Pfads ein dazugehöriges Trajektoid konstruiert. Der Algorithmus ist frei verfügbar und kann von allen genutzt werden. »Für jeden Pfad kann man immer eine Kugel mit einem Radius finden, die nach zwei Perioden ihre 3-D-Ausrichtung wiederherstellt«, sagte Sobolev zu »New Scientist«. »So kann man ein Objekt konstruieren, das ewig bergab rollt und immer wieder derselben Kurve folgt.« Dass das wirklich für so gut wie jeden Pfad möglich ist, konnten die Forscher nicht mathematisch beweisen. Aber sie vermuten, dass Ausnahmen »unendlich selten sind«, wie sie in ihrer Arbeit erklären. Denn als sie zufällige Pfade von Computern generieren ließen, waren sie jedes Mal in der Lage, ein dazugehöriges Trajektoid zu erzeugen.

Trajektoide in der Praxis

Um ihre Ergebnisse zu prüfen, haben die Forscher vorhergesagte Figuren mit Hilfe eines 3-D-Druckers ausgedruckt und schiefe Ebenen hinabrollen lassen. Und tatsächlich folgten die Objekte den vorgegebenen Pfaden. Damit eröffnen sich viel versprechende Anwendungen im Bereich der Robotik. »Deformierbare Roboter könnten auf diese Weise durch komplexe Landschaften und Hindernisse navigieren«, schreiben die Physiker Elisabetta Matsumoto vom Georgia Institute of Technology und Henry Segerman von der Oklahoma State University.

Aber auch abseits der Robotik gibt es spannende Ideen. In der Physik werden viele quantenmechanische Eigenschaften von Teilchen durch einen Punkt auf einer Kugeloberfläche dargestellt, zum Beispiel der Spin eines Teilchens. Verfolgt man die Veränderung des Spins (hervorgerufen etwa durch ein starkes Magnetfeld in einem Kernspintomografen oder durch logische Gatter innerhalb eines Quantencomputers), dann folgt der Punkt auf der Kugeloberfläche einer Kurve – ähnlich wie der Pfad eines Trajektoids. Somit lassen sich solche Zustandsänderungen von Teilchen durch geometrische Figuren darstellen. »Trajektoide, die so konstruiert wurden, dass sie die Spindynamik – und damit die Magnetfelder – in Magnetresonanztomografen steuern, könnten bei helfen, Nutzsignale von Rauschen zu trennen«, erklären Matsumoto und Segerman.