Im März 2023 sorgte eine mathematische Entdeckung für Schlagzeilen auch abseits der Fachwelt: »New York Times«, CNN, »Süddeutsche Zeitung« und andere berichteten über die 13-seitige geometrische Form, die manche an einen Hut und andere an ein T-Shirt erinnert. Mit diesem Vieleck kann man eine Ebene lückenlos bedecken – und das sich ergebende Muster ist dabei stets nicht periodisch.

Eine Form, die diese beiden Anforderungen erfüllt, wird als Einstein-Kachel bezeichnet (der Name leitet sich von »ein Stein« ab und hat nichts mit dem berühmten Physiker zu tun). Eine solche hatten Mathematikerinnen und Mathematiker seit Jahrzehnten gesucht, und einige hatten die Hoffnung darauf bereits aufgegeben. »Mich hat vor allem die Einfachheit der Form überrascht«, sagt der Mathematiker Michaël Rao von der École normale superieure in Lyon.

Einen Wermutstropfen hatte die im Frühjahr 2023 vorgestellte Hut-Kachel aber: Damit sie die Ebene lückenlos füllt, muss man Spiegelungen des 13-Ecks zulassen. »Die große Frage war, ob auch eine Einstein-Kachel existiert, die man nicht spiegeln muss«, erklärt Rao. Eine solche Form bezeichnen manche als »Vampir-Kachel«, da sie wie die mythische Nachtgestalt kein Spiegelbild besitzt. Eine solche Vampir-Fliese haben die Entdecker der Hut-Kachel, David Smith, Joseph Samuel Myers, Craig S. Kaplan und Chaim Goodman-Strauss, nun in einer noch nicht begutachteten Arbeit auf der Preprintplattform ArXiv vorgestellt.

Wieder ist es ein Hobby-Mathematiker, der die Vampir-Kachel findet

Wie das Team in seiner früheren Veröffentlichung feststellte, lassen sich durch Veränderungen der Kantenlängen des Huts weitere Fliesenformen finden, die ebenfalls lückenlose Pflasterungen erzeugen. Als der pensionierte Druckanlagentechniker David Smith eine dieser Fliesenformen aus Papier zurechtgeschnitten hatte und damit herumspielte, fiel ihm etwas Spannendes auf: Wenn er die Kacheln zusammensetzte, ohne sie zu spiegeln, schien sich ein lückenloses, nicht periodisches Muster zu ergeben.

»Natürlich begannen (Joseph Samuel Myers, Chaim Goodman-Strauss und ich) uns intensiver mit dieser Form zu beschäftigen«, schreibt der Informatiker Kaplan bei Mastodon. Nach einigen Monaten Arbeit konnten er und seine beiden Kollegen ihren Verdacht beweisen: Die von Smith untersuchte Kachel ermöglicht bloß nicht periodische Kachelungen, wenn man keine gespiegelten Teile zulässt.

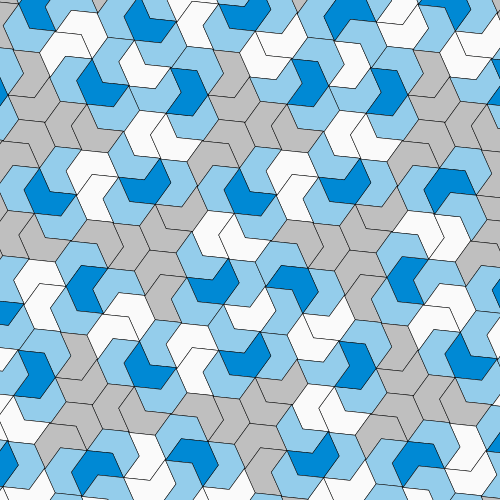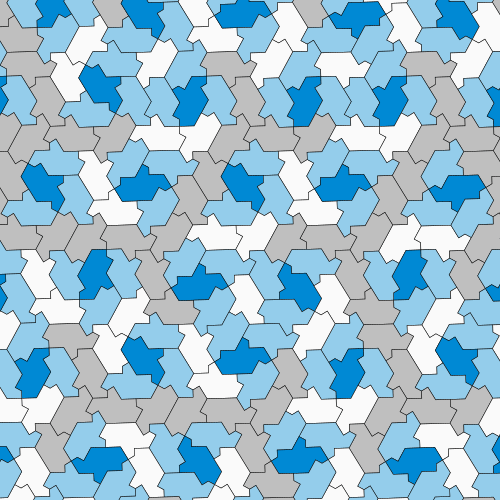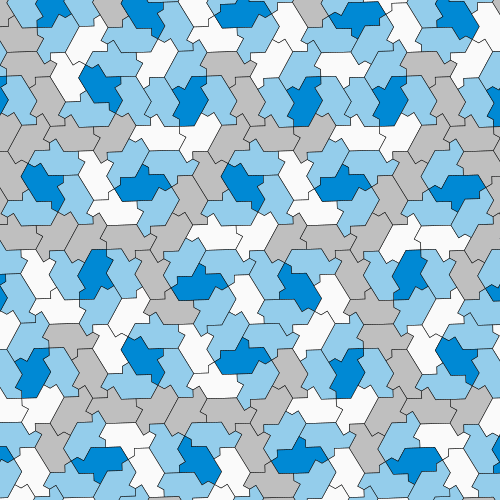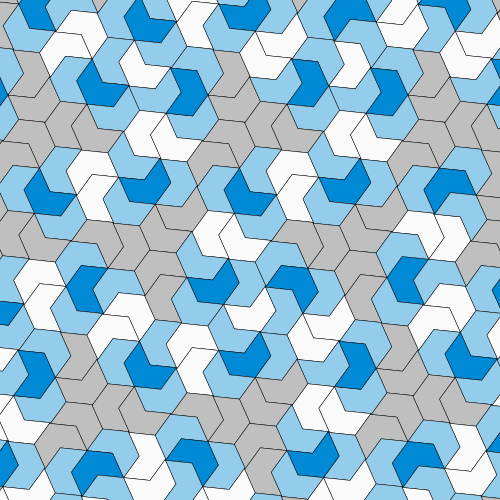
Doch ganz zufrieden waren die Wissenschaftler damit nicht. Denn: Fügt man gespiegelte Versionen der neuen Kachel ein, dann lassen sich auch periodische Muster erzeugen. Deswegen haben sie die Form des 13-Ecks verändert und die Ecken abgerundet, so dass eine neue Fliese entstand, die eher einem Puzzleteil ähnelt. Diese Kachel, die sie »Spectre« nennen, kann eine Ebene nur dann lückenlos bedecken, wenn man keine gespiegelten Versionen zulässt. Und die erzeugten Muster sind zwangsläufig nicht periodisch. Damit haben die Forscher nach eigenen Angaben eine Vampir-Fliese gefunden: einen zusammenhängenden Einstein, der kein Spiegelbild braucht, um eine Ebene lückenlos und zwangsweise nicht periodisch zu pflastern.

Denn einige Fachleute waren nicht zufrieden damit, dass die im März 2023 vorgestellte Hut-Kachel gespiegelt werden muss. »Das Problem ist nicht nur, dass sie gespiegelt auftaucht«, sagt der Mathematiker Michael Baake von der Universität Bielefeld, »sondern, dass eine der beiden Versionen – gespiegelt oder nicht gespiegelt – in einer Kachelung zwangsweise häufiger auftritt als die andere.« Dieses Problem hängt mit einer besonderen Eigenschaft von aperiodischen Mustern zusammen: Wer auf einer Ebene steht, die auf aperiodische Weise gekachelt ist, kann anhand des Musters nicht beurteilen, in welchem Bereich der Ebene er sich befindet oder um welche Art der Kachelung es sich handelt – aus einem Einstein lassen sich unendlich viele verschiedene Kachelungen erzeugen. Da es aber Hut-Parkettierungen mit überwiegend gespiegelten oder überwiegend nicht gespiegelten Kacheln gibt, lässt sich zumindest zwischen diesen zwei Varianten unterscheiden. Das widerspricht aber dem eigentlichen Merkmal von aperiodischen Parkettierungen, die überhaupt keine Unterscheidungen erlauben.

Die neu entdeckte Spectre-Kachel scheint hingegen alle Anforderungen an einen Einstein zu erfüllen: Es handelt sich um eine einzige zusammenhängende Fliese, die entlang der Ebene lediglich rotiert und verschoben wird und dabei ein lückenloses, stets unregelmäßiges Muster erzeugt. Und da sie ohne Spiegelung auskommt, ist es auch für Fliesenhersteller einfacher, die Kacheln für ein perfektes Nerd-Badezimmer herzustellen.

Zurücklehnen können sich Mathematikerinnen und Mathematiker aber noch nicht. »Es wäre interessant, herauszufinden, wie viele Seiten eine Einstein-Kachel mindestens braucht«, sagt Rao. »Oder ob eine rein aperiodische Kachel auch ein Polygon sein kann.« Das neue Ziel ist also, eine möglichst einfache Einstein-Kachel zu finden. Die Jagd ist eröffnet.