19 Kreise im Kreis
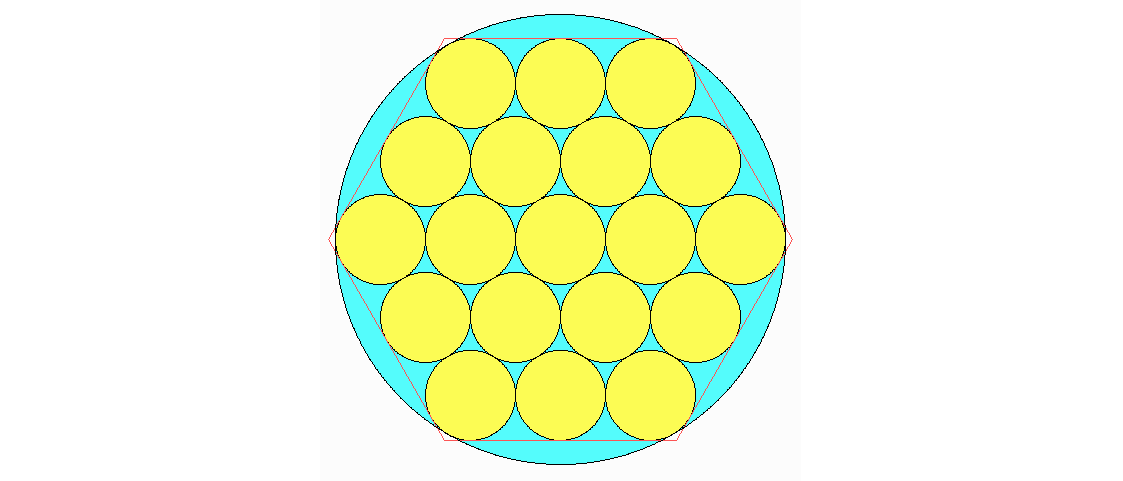
Es ist ja kein Kunststück, 19 gleiche Kreise (oder 7 oder 37 oder 61 und so weiter) nebeneinander in ein möglichst kleines reguläres Sechseck zu legen.
Die kleinen Kreise werden dabei von einem großen Kreis umschlossen, der nur 6 von ihnen berührt und vom Sechseck kleine Zipfel abschneidet. Kann man die 19 kleinen Kreise so verschieben, dass sie zwar nicht mehr in das Sechseck passen, aber dafür in einen etwas kleineren Kreis?
Ein Zwölfeck voller Symmetrie!
19 Kreise
Die Animation zeigt es schrittweise: Wir schieben erst die Kreise nach außen, die noch nicht den Kreis berühren, drehen dann die inneren sieben Kreise um 15° und ziehen dann den äußeren Kranz etwas enger. Man glaubt es nicht, bevor man es gesehen hat!
Das Ergebnis ist dann folgendes:
Das sieht doch schon einmal sehr schön symmetrisch aus, aber wie verhalten sich nun die Radien, wenn \(r\) der Radius eines kleinen Kreises ist?
Wie man zum Beispiel im Fünfeck 1-3-10-11-4 aus dem Quadrat 1-10-11-4 und dem gleichseitigen Dreieck 1-3-4 sehen kann, ist die Entfernung \(z\) zwischen den Punkten 1 und 11 oder, was dasselbe ist, der Umkreisradius des Zwölfecks, das aus den Mittelpunkten der zwölf äußeren Kreise besteht: \(z = 2r\sqrt{2 + \sqrt{3}}\) (Pythagoras im rechtwinkligen Dreieck 1 – 10 – Mittelpunkt von 10 und 11).
Der Radius des großen Kreises ist um ein \(r\) größer, also etwa \(4{,}8637 r\).
Kravitz hat 1967 bewiesen, dass diese Figur die optimale Lösung ist, wenn man 19 Kreise nebeneinander in einem möglichst kleinen Kreis unterbringen möchte.
Zum Schluss noch einmal die Animation – jetzt aber mit Linien, die anzeigen, welche Kreise sich berühren.
Was ist nun in diesem Zusammenhang das Besondere an der Zahl 19? Offenbar ist es bedeutsam, dass 19 = 1 + 6 + 12 ist. Das kann man fortsetzen zu der arithmetischen Folge zweiter Ordnung, bei der die Differenzen der Reihe nach Vielfache von 6 sind, also:
1 = 1
7 = 1 + 6
19 = 1 + 6 + 12
37 = 1 + 6 + 12 + 18
61 = 1 + 6 + 12 + 18 + 24
91 = 1 + 6 + 12 + 18 + 24 + 30
127 = 1 + 6 + 12 + 18 + 24 + 30 + 36
und so weiter ...
Diese Zahlen 1, 7, 19, 37 und so weiter heißen aus naheliegenden Gründen "Sechseckzahlen". Für jede davon ist es ziemlich einfach, die entsprechende Anzahl von gleichen Kreisen in ein möglichst kleines regelmäßiges Sechseck zu packen:
Können Sie sie nun auch platzsparend in Kreise packen, wie es beim 19-Eck durch die Umlagerung zum regelmäßigen 12-Eck gelungen ist?
37 Kreise
37 = 1 + 6 + 12 + 18. Daher nehmen wir nun ein reguläres 18-Eck, aber statt der Quadrate brauchen wir nun Rauten mit Winkeln, die durch 20° teilbar sind.
Hier springt die wunderbare Symmetrie noch nicht in die Augen.
Im nächsten Bild sind Winkelskalen mit 20° Teilung eingezeichnet. Alle Verbindungslinien folgen diesem Winkelraster, wie Sie leicht nachzählen können, wenn Sie bedenken, dass man beim Umfahren eines regelmäßigen 18-Ecks an jeder Ecke seine Richtung um 20° ändern muss.
Zur Verdeutlichung sind hier für 1/6 der rotationssymmetrischen Figur gleiche Winkel durch gleiche Farben markiert. Es gibt also 18 gleichseitige Dreiecke und ebenso viele Rauten mit den Winkeln 80° und 100°.
Auf wie vielen Kreisen liegen die Mittelpunkte der kleinen Kreise?
Die Mittelpunkte 2 bis 7 und 20 bis 37 liegen auf zwei Kreisen, aber 8 bis 13 liegen auf einem etwas kleineren als 14 bis 19, sonst würden sie nicht zwischen die vorher genannten passen! Immerhin schließen sich die Kreise 20 bis 37 nahtlos zu einem Kranz und berühren allesamt den großen Umkreis.
Man kann die minimale Packung auch so beginnen, dass man die Kränze mit 1, 6, 12 und 18 Kreisen umeinander legt. Allerdings wird es dann schwierig, die Kränze so gegeneinander zu verdrehen, dass man die Lücken optimal nutzen und die Radien der Kränze minimieren kann. Mit den Rauten ist es dagegen ganz einfach. Zugleich haben wir eine hinreißend schöne Zerlegung des regelmäßigen 18-Ecks.
61 Kreise
Nun stellt sich fast von selbst die Frage: Können wir nicht noch einen Kranz außen herum legen und damit zum 24-Eck mit der Packung von 61 Kreisen in einen kommen?
Jein. Wir müssen die bisherigen Kränze etwas anders organisieren, denn im regelmäßigen 24-Eck sind alle Winkel (auch für die schönen Rauten darin!) durch 15° teilbar. Es treten sogar Quadrate darin auf. Das Ergebnis ist dann folgendes:
Dieses ist – wie man stark vermutet – eine von mehreren gleich guten Möglichkeiten, 61 gleiche Kreise nebeneinander in einen möglichst kleinen Kreis zu legen. Zugleich haben wir es hier mit einer Zerlegung des regelmäßigen 24-Ecks in 24 gleichseitige Dreiecke, 12 Quadrate und 24 Rauten mit den Winkeln 75° und 105° zu tun.
Das Spiel kann man noch fortsetzen, und zwar mit den regelmäßigen \(6n\)-Polygonen und den Rauten darin. Die zugehörigen Kreise sind aber nur noch für \(n = 5\) (\(1 + 6 +12 + 18 + 24 +30 = 91\) Kreise) und \(n = 6\) (\(1 + 6+ 12 + 18 + 24 + 30 + 36 = 127\) Kreise) optimale Kreispackungen: für \(169\) Kreise und weitere Glieder dieser arithmetischen Folge sehen die Kreispackungen zwar immer noch schön aus, werden aber von ausgesprochen hässlichen unregelmäßigen Figuren an Platzausnutzung überboten.
91 Kreise
Hier ist erst einmal die optimale Packung für 91 Kreise in Verbindung mit der Zerlegung des regelmäßigen 30-Ecks in gleichseitige Dreiecke und Rauten mit Winkeln, die durch 12° teilbar sind:
127 Kreise
Und ganz zum Schluss noch 127 optimal eingefüllte Kreise mit der Zerlegung des 36-Ecks, unter anderem in 18 Quadrate und auch sonst im 10°-Winkelraster:
Man sieht hier deutlich, wie die einzelnen Kränze von innen nach außen vom Sechseck ausgehend immer "runder" werden.
Beachten Sie bitte, dass zum Beispiel die inneren 91 Kreise von den 127 etwas anders liegen als bei der Lösung des 91-Kreise-Problems. Insbesondere ist bei letzterer schon der äußerste Kranz mit den 30 Kreisen genau rund, das heißt die Mittelpunkte seiner Kreise liegen auf einem Kreis, was sonst nur noch für das innerste Sechseck zutrifft. Die Kränze dazwischen vermitteln auf eine raffinierte Weise durch Kompromisse zwischen Sechseck und Kreis, um den Platz zu optimieren. In bemerkenswerter Weise ist dabei der äußerste – runde – Kranz lückenlos geschlossen. Verstehen kann man das ganz einfach mit der Rautenkonstruktion auf der Basis der rationalen Winkelverhältnisse.
Zusammenfassendes Ergebnis
Lassen wir noch einmal die Lösungen für 19, 37, 61, 91 und 127 Kreise Revue passieren:Und nun in der gleichen Reihenfolge die Sortierung der Rauten:
... und schließlich noch die Zerlegungen der regelmäßigen Polygone mit 12, 18, 24, 30 und 36 Ecken:
Quadrate kommen beim 12-Eck, 24-Eck und 36-Eck vor.
Alternative Herangehensweise
Eine etwas andere Möglichkeit die Aufgabe zu lösen, besteht darin, dass man ein ebenes Gelenkpolygon aus gleichseitigen Dreiecken und Rauten betrachtet, die geschlossene Ringe um die Mitte bilden mit \(1 + 6 + 12 + 18\) und so weiter Gelenken. Die Gelenke des jeweils äußersten Rings können dann gemeinsam etwas rundherum gleiten, wobei der Umfang streng konstant bleibt und gelegentlich Drehsymmetrie auftreten kann. Geht man vom Sechseck aus, so bestehen alle Rauten aus zwei gleichseitigen Dreiecken:
Da in diesem Beispiel der äußerste Ring aus 24 Gelenken (beziehungsweise Kreisen) besteht, dreht man von innen nach außen jeden Ring gegen den nächst-inneren um 360°/24 – wobei der von dieser Drehung betroffene Ring und alle weiter außen befindlichen ihre Form ändern:
In der Animation sieht das so aus:
Für 91 Kreise (beziehungsweise Gelenke) muss man – wegen der 30 Kreise im äußersten Ring – jeden Ring um 10° weiter drehen als den jeweils innen benachbarten:
Hier ist besonders schön zu sehen, wie durch das gezielte Auflockern aus dem dichtest gefüllten großen Sechseck ein gefüllter Kreis wird, der kleiner als der ehemalige Hüllkreis ist. Es sei aber noch einmal betont, dass unabhängig davon gezeigt werden muss, ob diese Kreispackung nicht durch eine weniger symmetrische übertroffen wird.
Websites über die Packung von Kreisen in Kreise, Quadrate bzw. auch in Sechsecke sind vor allem auf der Webseite "Packomania" aus der Universität Magdeburg.
Ich muss zugeben, dass mich an den Kreispackungen die symmetrischen Lösungen – vor allem solche, deren Symmetrie ein näheres Hinsehen erfordert – mehr faszinieren als die bloße Optimierung.
Schreiben Sie uns!
1 Beitrag anzeigen