Bang
Jedes (auch unregelmäßige) Tetraeder hat eine Inkugel – eine Kugel, die alle vier Flächen des Polyeders berührt. Von den Berührpunkten der Flächen mit dieser Kugel gibt es zu den Ecken auf jeder der 4 Flächen die gleichen drei Winkel. Können Sie das zeigen?
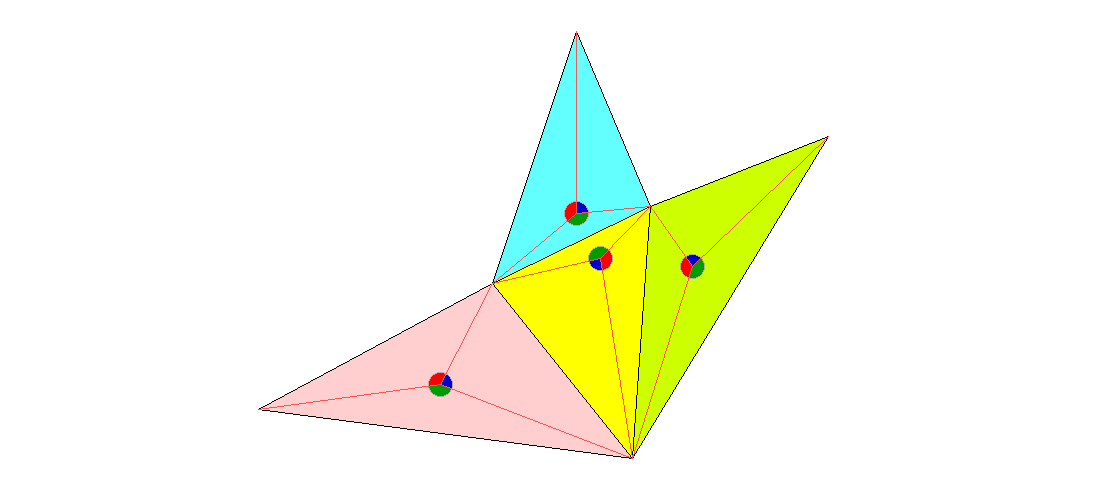
Das Bild zeigt alle 4 Flächen in eine Ebene geklappt und führt zur Begründung.
Welche der 12 kleinen Dreiecke sind jeweils zueinander deckungsgleich?
Von jeder Ecke aus ist es zu den drei anliegenden Berührpunkten mit der Kugel gleich weit. Daraus folgt, dass von den 12 kleinen Dreiecken jeweils zwei zueinander deckungsgleich sind, die eine Tetraederkante gemeinsam haben.
Damit haben wir es bei den fraglichen 12 Winkeln – von denen gezeigt werden soll, dass sie nur drei verschiedene Werte haben – mit 6 Paaren von je gleichen Werten zu tun, hier farblich unterschieden.
In jedem der 4 Berührpunkte ergeben drei davon zusammen 180o. Nennen wir sie nach den Anfangsbuchstaben der verwendeten Farben (blau, grün, rot, orange, violett, cyan), so haben wir \(b + g + r \)\(= v + c + r \)\(= g + v + o \)\(= b + c + o\). Also sind \(b + g = v + c\) und (\g + v = b + c\). Daraus ergibt sich \(b – v = v – b\), also \(v = b\).
In gleicher Weise finden wir auch \(r = o\) und \(g = c\).
Der hier gezeigte Satz wurde 1897 von Bang vermutet und im selben Jahr von Gehrke bewiesen. Trotzdem wird er als "Satz von Bang" bezeichnet – vielleicht nicht so ungerecht, wie es scheint: Der Beweis ist möglicherweise einfacher als die Idee zu der Vermutung. Er wird in Honsbergers Gems II im 9. Kapitel behandelt.
Übrigens hat man beim Anfertigen der Zeichnung einige Freiheit: Zwei der Dreiecksflächen des Tetraeders (also 5 der 6 Kanten) und ein Berührpunkt mit der Inkugel sind frei wählbar. Der Rest liegt dann fest.
Schreiben Sie uns!
Beitrag schreiben