Hemmes mathematische Rätsel: Crux Numerorum
Die Mitglieder der mathematischen Gesellschaft der altehrwürdigen englischen Universität Cambridge haben sich den klangvollen Namen »Archimedier« gegeben. Seit 1939 geben sie etwa einmal pro Jahr eine Zeitschrift mit dem Titel Eureka heraus. In ihr veröffentlichen Studenten und Mathematiker aus der ganzen Welt Artikel aus allen Bereichen der Mathematik, aber auch über Denksportaufgaben und Puzzles. Viele berühmte Mathematiker und Physiker wie Paul Erdős, Martin Gardner, Douglas Hofstadter, Godfrey Hardy, Béla Bollobás, John Conway, Roger Penrose, Ian Stewart, Timothy Gowers, Stephen Hawking und Paul Dirac haben für die bislang erschienenen 64 Hefte von Eureka Aufsätze geschrieben. In der im März 1993 herausgegebenen 52. Ausgabe von Eureka stellt ein nicht bekannter Autor unter dem Pseudonym Ampenditus ein Kreuzzahlrätsel.
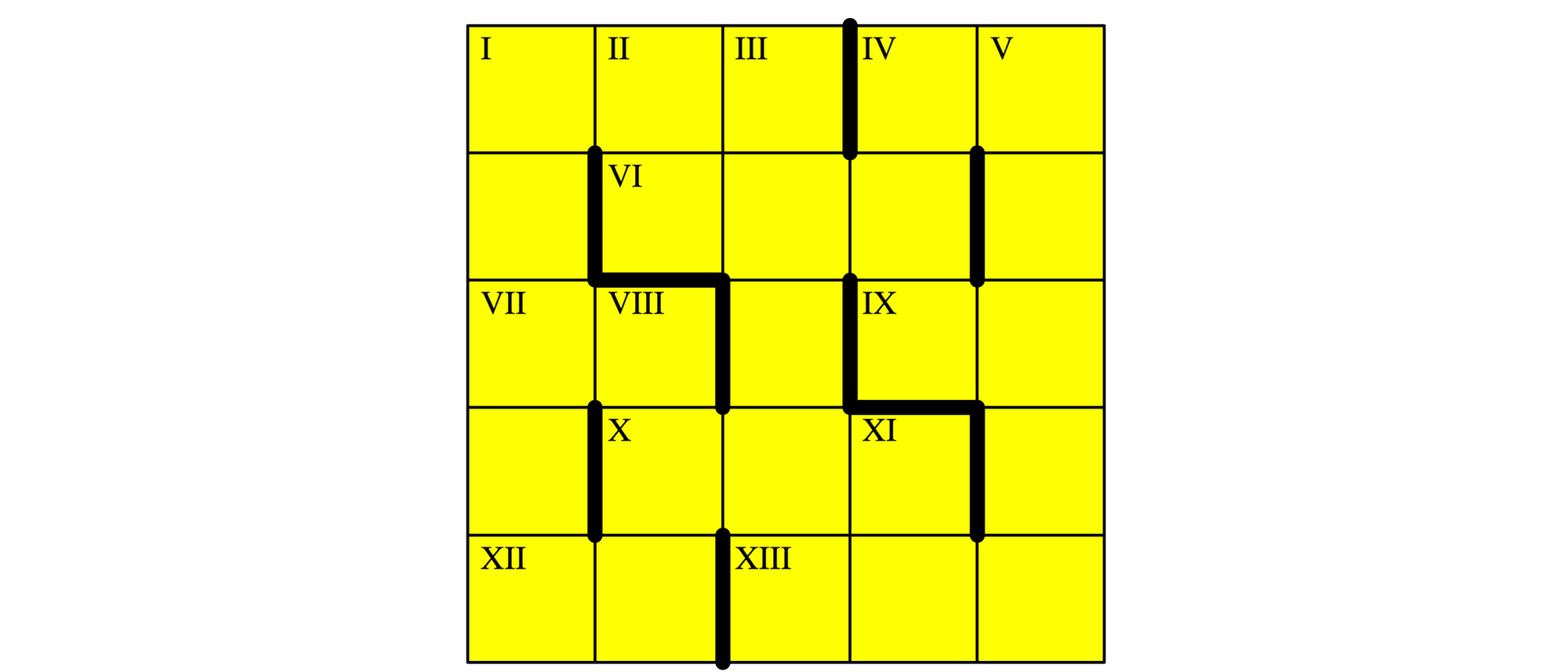
Setzen Sie in jedes Feld ein römisches Zahlenzeichen, so dass waagerecht und senkrecht gültige römische Zahlen in Standardnotation entstehen. Die fetten Striche trennen zwei Zahlen. Kein Zeichen ist größer als C. Außerdem gilt:
Iw = VIw + XIIw
Is = Xw • Vs
IIIs = VIIw + VIIIs
IVw = IXw • XIs
(w = waagerecht, s = senkrecht)
Die vierte Bedingung des Kreuzzahlrätsels verlangt, dass IV waagerecht das Produkt aus IX waagerecht und XI senkrecht sein soll. Alle drei Zahlen sind zweistellig. Da die Zeichen D und M nicht erlaubt sind, können dies nur II, IV, VI, IX, XI, XV, IX, XL, LI, LV, LX, XC, CI, CV, CX, CL, XC und CC sein. Daraus lassen sich nur die Produkte XL = II • XX, LX = IV • XV und XC = VI • XV bilden. Nach der zweiten Bedingung ist I senkrecht das Produkt aus V senkrecht und X waagerecht. Da I waagerecht höchstens CCCLX sein kann und V senkrecht mindestens XVIII sein muss, kommen für X waagerecht nur die Zahlen III, VII, XII, XIV, XVI und XIX in Frage. V senkrecht kann nicht mit C beginnen, denn man kann leicht überprüfen, dass dann alle ganzzahligen Vielfachen dieser Zahl niemals I senkrecht sein können. Die größte fünfstellige Zahl, die nicht mit C beginnt, ist XCVII. Da CCCLX : XCVII = 4 ist, kann X waagerecht nur III sein. Folglich kann IV waagerecht nur XL oder LX, IX waagerecht nur XX oder XV und XI senkrecht nur II oder IV sein. Der Rest ist jetzt nicht mehr schwer, und es gibt drei verschiedene Lösungen.
Schreiben Sie uns!
Beitrag schreiben