Hemmes mathematische Rätsel: Das Kreissehnenprodukt
Das »Mathematics Magazine« wird seit 1947 von der »Mathematical Association of America« herausgegeben und erscheint alle zwei Monate. Es wendet sich mit unterhaltsamen mathematischen Artikeln an Mathematiklehrer und -studenten. Die Zeitschrift stellt ihren Lesern auch in jeder Ausgabe eine ganze Reihe von mathematischen Denksportaufgaben. Im Februar 1995 veröffentlichten Andre P. Mazzoleni von der Texas Christian University mit Samuel Shan-Pu Shen von der University of Alberta in Kanada im »Mathematics Magazine« ein Kreissehnenproblem und seine Lösung.
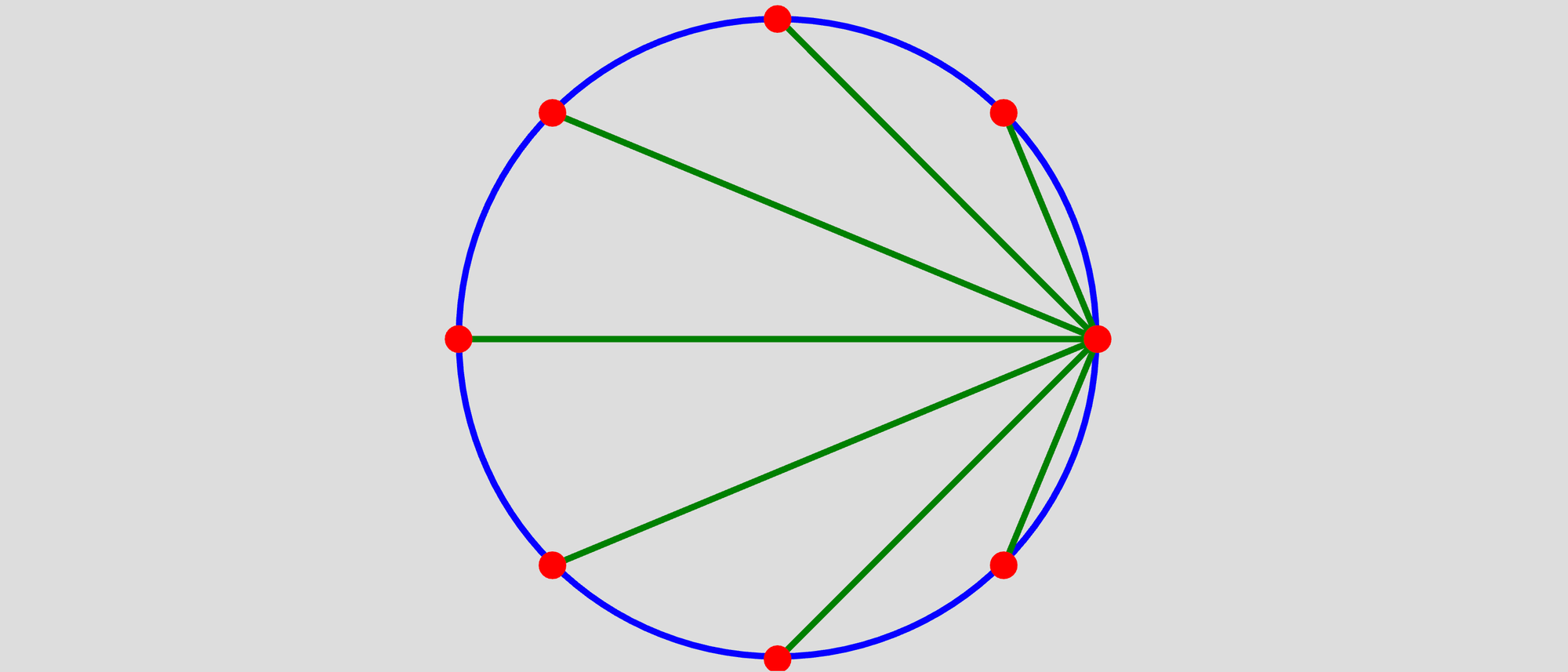
Bei einem Kreis mit dem Radius 1 liegen auf dem Umfang acht rote Punkte, die jeweils gleiche Abstände von ihren Nachbarn haben. Einer der Punkte ist durch sieben Sehnen mit den anderen sieben Punkten verbunden. Wie groß ist das Produkt der sieben Sehnenlängen?
Der Radius des Kreises ist 1. Folglich haben die Strecken MA, MB, MC und ME auch die Länge 1. Für das rechtwinklige Dreieck ACM erhält man daher mit dem Satz des Pythagoras AC2 = 2.
Da die Strecke MC rechtwinklig auf MA steht und die Punkte C, B und A jeweils den gleichen Abstand haben, beträgt der Winkel AMB 45°. Nun kann man den Kosinussatz auf das Dreieck ABM anwenden: AB2 = MA2 + MB2 – 2 • MA • MB • cos 45°. Die Gleichung kann man zu AB2 = 1 + 1 – 2 • cos 45° vereinfachen. Der Kosinus von 45° beträgt ½√2. Setzt man dies in die Gleichung ein, erhält man AB2 = 2 – √2.
Die Hypotenuse des Dreiecks ADE ist ein Durchmesser des Kreises. Somit ist nach dem Satz des Thales das Dreieck rechtwinklig und es gilt DE2 + AD2 = AE2. Die Strecken AB und DE sind gleich lang. Folglich ist AB2 + AD2 = 22 oder AD2 = 4 – AB2 = 4 – (2 – √2) = 2 + √2.
Das Produkt der sieben Sehnenlängen ist P = AB • AC • AD • AE • AF • AG • AH. Da AB = AH, AC = AG und AD = AF ist, vereinfacht sich die Gleichung zu P = AB2 • AC2 • AD2 • AE. Nun werden die Sehnenlängen eingesetzt und ergeben P = (2 – √2) • 2 • (2 + √2) • 2 = 8.
Schreiben Sie uns!
Beitrag schreiben