David Wells wurde 1940 in England geboren. Er studierte Mathematik an der Universität Cambridge, brach aber sein Studium ab und ließ sich danach zum Lehrer ausbilden. Während seines Studiums wurde er britischer Schachmeister der unter 21-jährigen Spieler. In den Siebzigerjahren des letzten Jahrhunderts entwickelte er einige recht erfolgreiche Spiele wie Guerilla, Galaxis und Checkpoint: Danger!. Er hat zahlreiche Knobeleien erfunden und betreute in den 70er Jahren die Denksportredaktion der Zeitschrift Games and Puzzles. Von 1981 bis 1983 gab er eine eigene Zeitschrift heraus mit dem Titel The Problem Solver. Wells hat etliche Bücher zur Unterhaltungsmathematik geschrieben, die zum Teil auch auf Deutsch erhältlich sind. Sein bekanntestes Werk ist das Lexikon der Zahlen. Das heutige Rätsel veröffentlichte er im Februar 1975 in der Zeitschrift Games and Puzzles.

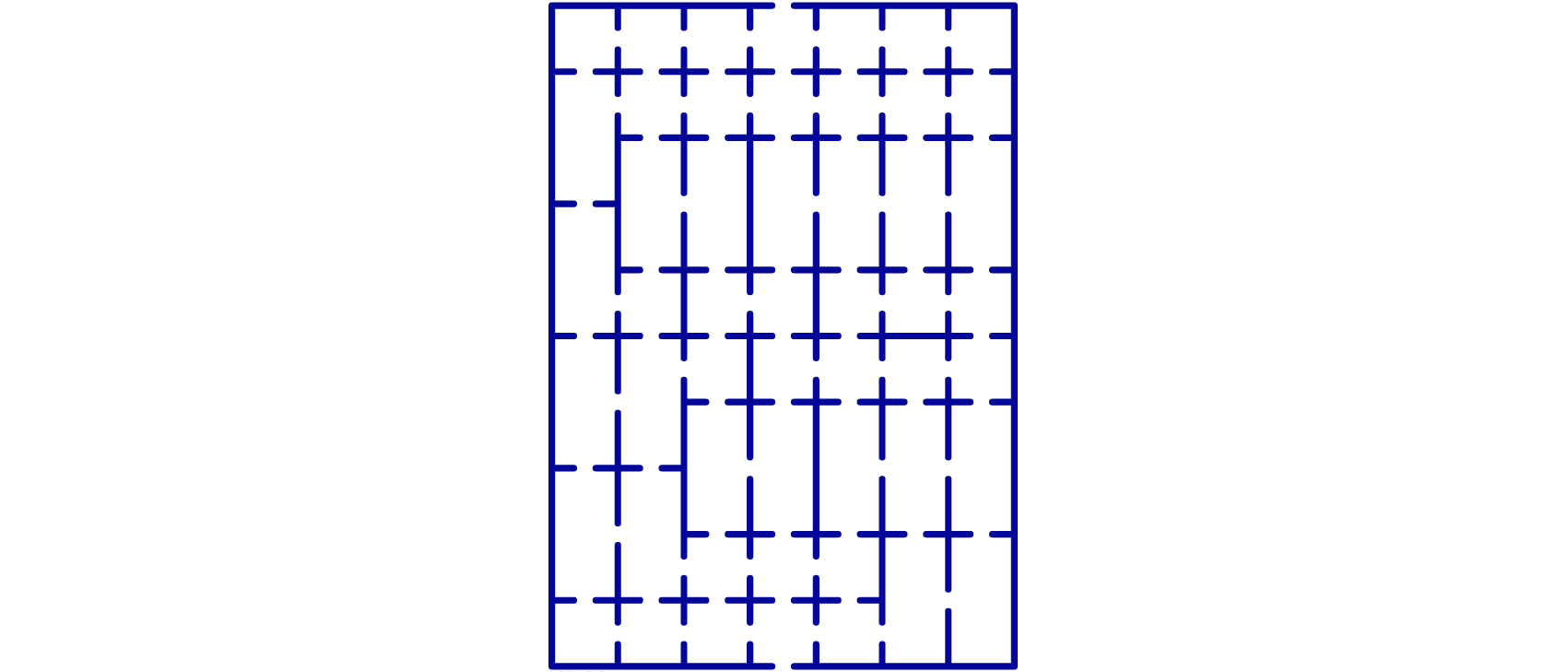
Theseus betritt das Labyrinth, in dem der Minotaurus auf ihn lauert, durch den südlichen Eingang und will es durch den nördlichen, an dem Ariadne auf ihn wartet, wieder verlassen. Um das Ungeheuer zu verwirren, verlässt Theseus keinen Raum, in den er hineingeht, durch den gegenüberliegenden Ausgang, sondern biegt jedesmal links oder rechts ab. Welches ist der kürzeste derartige Weg durch das Labyrinth? Es soll dabei angenommen werden, dass Theseus immer parallel oder quer zu den Wänden der Räume geht.