Hemmes mathematische Rätsel: Das Logo des Piusgymnasiums
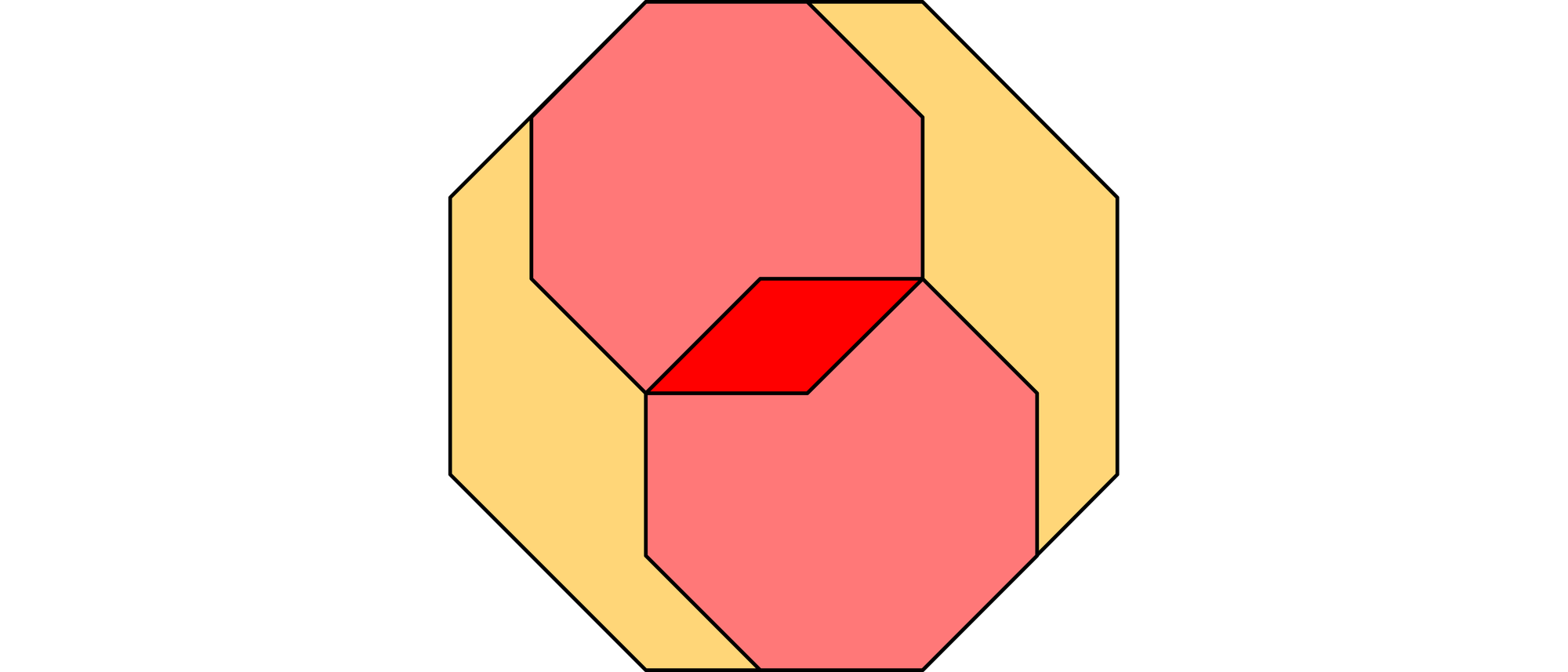
Im Januar 2003 gab mir jemand ein Faltblatt des Piusgymnasiums in Aachen. Dabei fiel mir das Logo der Schule auf, das aus einem regelmäßigen Achteck besteht, das die beiden Grußbuchstaben P und ein G umschlingt. Die zwei Buchstaben überlappen sich und haben beide auch eine achteckige Struktur. Vermutlich sollen diese drei Achtecke auf das Oktogon des Aachener Doms hinweisen.
Ich schuf dann aus diesem Logo eine Aufgabe, die ich im Mai 2003 in der Zeitschrift »Bild der Wissenschaft« veröffentlichte. Dazu vereinfachte ich das Logo ein wenig, indem ich einige Striche fortließ und alle Achtecke regelmäßig machte.
Wie lang sind die Seiten der kleinen Achtecke, wenn das große Achteck eine Seitenlänge von 10 cm hat?
Den Abstand von zwei sich gegenüberliegenden Seiten des äußeren Achtecks lässt sich auf zweierlei Weise bestimmen. Die beiden Ausdrücke, die man dabei erhält, kann man natürlich gleichsetzen: 2a + 3b = A + 2B. Die beiden Größen B und b entsprechen den Seitenlängen von Quadraten mit den Diagonalen A und a und haben folglich die Längen B = A/√2 und b = a/√2. Setzt man dies in die obige Gleichung ein und löst sie nach dem Seitenverhältnis auf, erhält man a/A = (2 + 2√2) / (4 + 3√2). Die Seitenlänge der kleinen Achtecke beträgt somit etwa 5,857 cm.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.