Hemmes mathematische Rätsel: Das quadrierte Rechteck
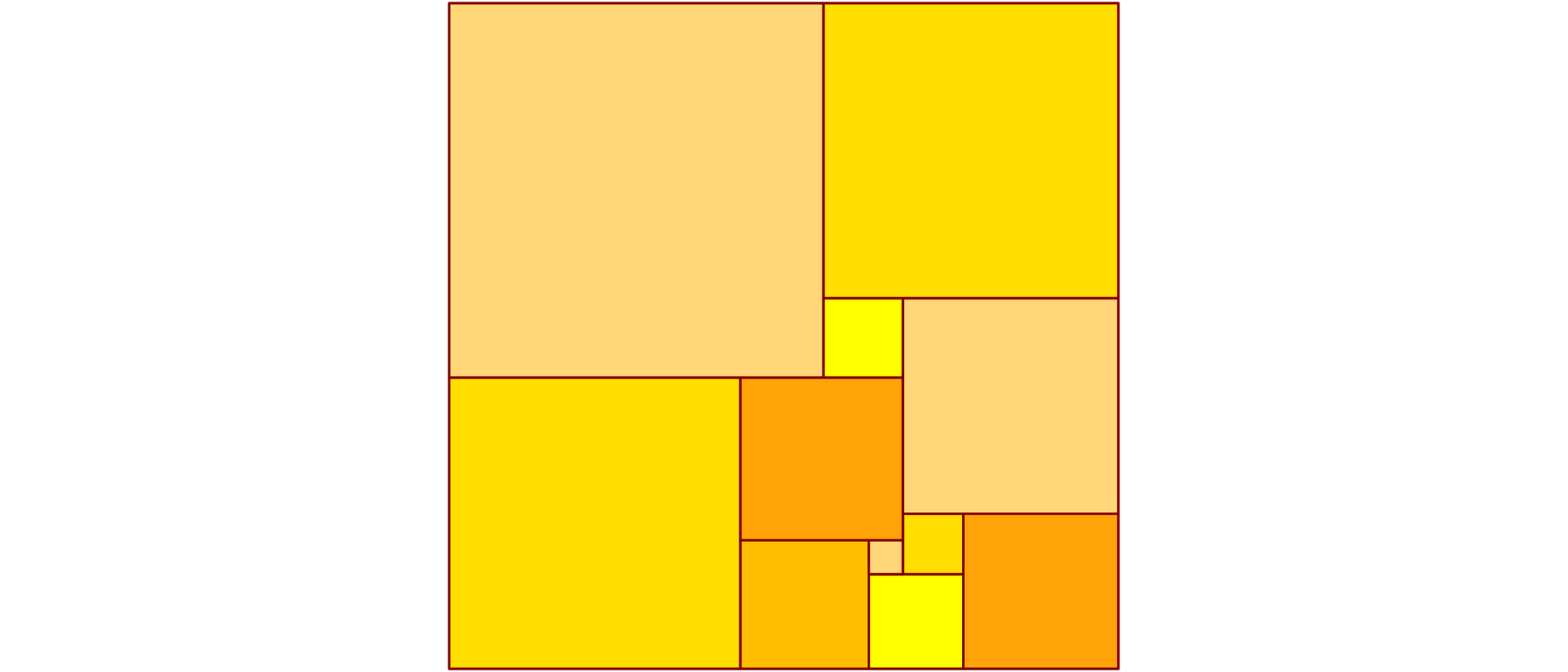
In den Jahren 1936 bis 1938 versuchten vier Mathematikstudenten an der Universität Cambridge Quadrate in lauter unterschiedlich große Quadrate zu unterteilen. Sie waren erfolgreich. Die Veröffentlichung ihrer Ergebnisse zog sich aber bis 1940 hin, so dass der Berliner Mathematiker Roland Sprague (1894-1967), der sich unabhängig davon auch mit dem Thema befasst hatte, ihnen zuvor kam und seine Quadratur des Quadrats bereits 1939 veröffentlichte. Einer der vier Cambridger Studenten war der 1916 geborene und 2000 gestorbene Engländer Arthur Harold Stone. Bei seinen Arbeiten an dem eigentlichen Problem fand er, gewissermaßen als Abfallprodukt, ein fast quadratisches Rechteck, das er in elf verschiedene Quadrate zerlegen konnte.
Dieses quadrierte Rechteck zierte 60 Jahre später eine Briefmarke im Wert von 110 Pfennigen, welche die Deutsche Post anlässlich des Internationalen Mathematiker-Kongresses herausgegeben hatte, der 1998 in Berlin stattfand. Diese Briefmarke wiederum regte den Mathematiker Jürgen Fischer von der Hochschule für Technik in Stuttgart an, seinen Studenten im März 2000 folgendes Preisrätsel zu stellen:
Alle Quadrate des Rechtecks auf der Briefmarke haben ganzzahlige Seitenlängen. Welches sind die kürzestmöglichen Seitenlängen, die das Rechteck haben kann?
Bezeichnet man die Seitenlängen der beiden kleinsten Quadrate mit a und b, so kann man damit die Seitenlängen aller anderen Quadrate ausdrücken. Das ist eine leichte Aufgabe, und die Ergebnisse finden Sie in den einzelnen Quadraten der Zeichnung.
Für das Quadrat oben links, für das noch keine Abmessungen in der Zeichnung zu sehen sind, ergibt sich dann als Länge seiner waagerechten Seite (5a + 2b) + (3a + b) − (–3a + 3b) = 11a und als Länge der senkrechten Seite (–2a + 6b) + (–3a + 3b) = –5a + 9b.
Damit die Fläche auch tatsächlich quadratisch ist, muss 11a = –5a + 9b oder 16a = 9b sein. Die kleinsten natürlichen Zahlen, die diese Bedingung erfüllen, sind a = 9 und b = 16. Nun kann man die Seitenlängen der neun anderen Quadrate leicht zu 21, 25, 34, 41, 43, 57, 77, 78 und 99 berechnen.
Daraus ergibt sich, dass das äußere Rechteck die Seitenlängen 176 und 177 haben muss.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.