Hemmes mathematische Rätsel: Das verschwundene Quadrat
Zerschneidet man eine ebene Figur und setzt die Teile zu einer anderen Form wieder zusammen, so sollte sich der Flächeninhalt dadurch nicht verändert haben. Der erste, der aus dieser doch so selbstverständlichen Tatsache ein Rätsel machte, war William Hooper.
Im vierten Band seines 1774 in London erschienenen Werks »Rational Recreations« vergrößerte scheinbar ein in vier Teile zerlegtes Rechteck seinen Flächeninhalt durch das Zusammensetzen zu einem Sechseck. Der Trick dabei war jedoch leicht zu durchschauen. Eine deutlich raffiniertere Version des Hooper'schen Vergrößerungsrätsels entwarf 1953 der New Yorker Amateurmathematiker Paul Curry.
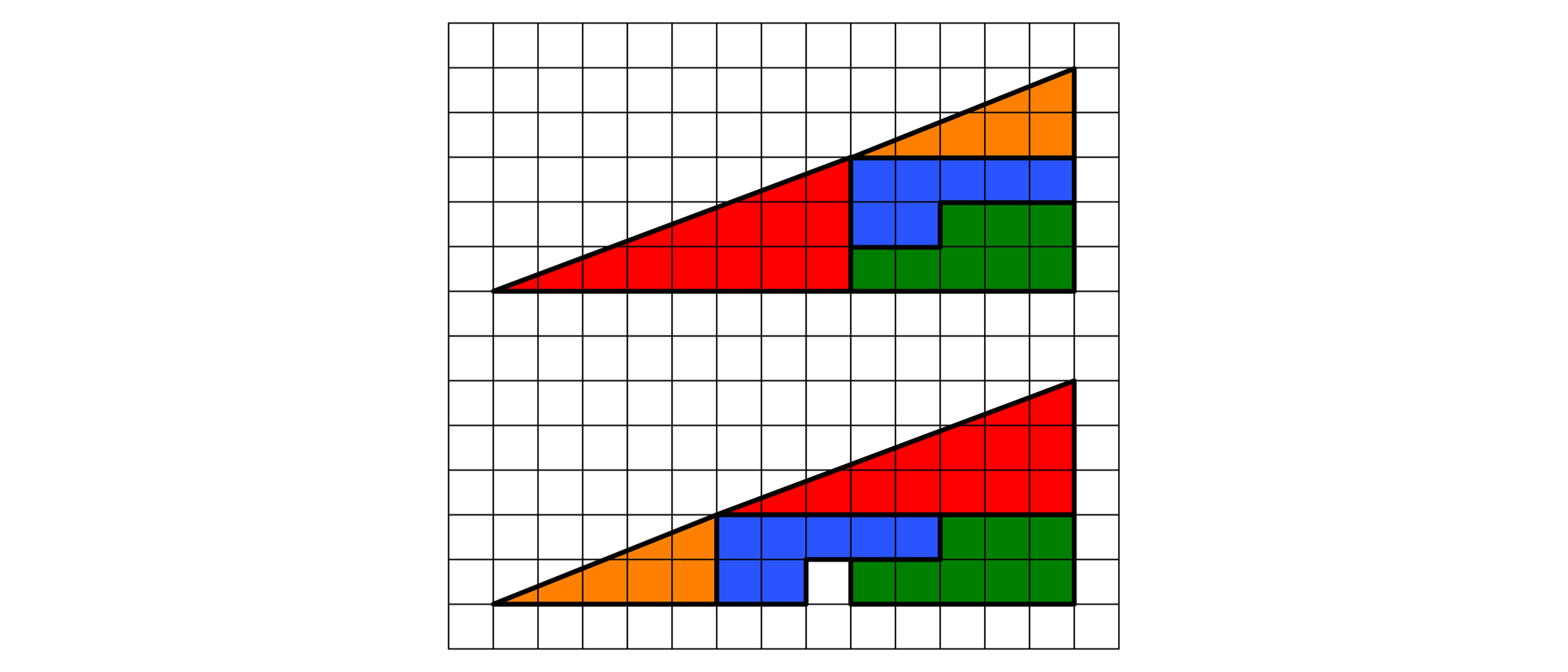
Er zerschnitt ein rechtwinkliges Dreieck, das einen Flächeninhalt von 32,5 Quadrateinheiten hatte, in zwei Dreiecke und zwei hakenförmige Sechsecke. Nachdem er sie auf eine etwas andere Weise zu dem gleichen rechtwinkligen Dreieck wieder zusammengesetzt hatte, blieb eine kleine quadratische Lücke in der Figur frei. Wohin ist dieses Quadrat verschwunden?
Der Trick bei dem Rätsel ist, dass das äußere Dreieck eigentlich gar kein Dreieck ist. Die »Hypotenuse« ist nämlich keine gerade Linie, sondern an der Stelle, an der die beiden kleinen Dreiecke aneinander stoßen, nach innen geknickt. In Wahrheit handelt es sich also um ein Viereck, das einen Flächeninhalt von 32 Quadrateinheiten hat.
Auch nach dem Zusammensetzen der vier Einzelteile zu der zweiten Figur, erhält man kein Dreieck, sondern wieder ein Viereck. Doch diesmal ist die »Hypotenuse« nach außen geknickt, so dass das Viereck jetzt einen Flächeninhalt von 33 Quadrateinheiten hat. Da sich aber natürlich der Flächeninhalt des ersten Viereckes durch das Zerschneiden und Umordnen nicht ändern kann, muss eine Quadrateinheit unbedeckt bleiben.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.