Hemmes mathematische Rätsel: Das Würfelgerüst
Seit Januar 1990 schreibe ich für das Magazin »bild der wissenschaft« die Kolumne »Cogito«. Dabei mündet immer eine kurze Geschichte über Dinge und Ereignisse des Alltagslebens in eine mathematische Denksportaufgabe. Die Geschichten liegen inzwischen auch als Rätselsammlungen in vier Büchern vor: »Mensch, ärgere dich nicht« (2003), »Alice im Knobelland« (2006), »Das flächenländische Triumvirat« (2010) und »Euklids Wohnzimmer« (2019). Die Rätselgeschichte, die ich im Dezember 1990 veröffentlichte, handelt von Spielwürfeln.
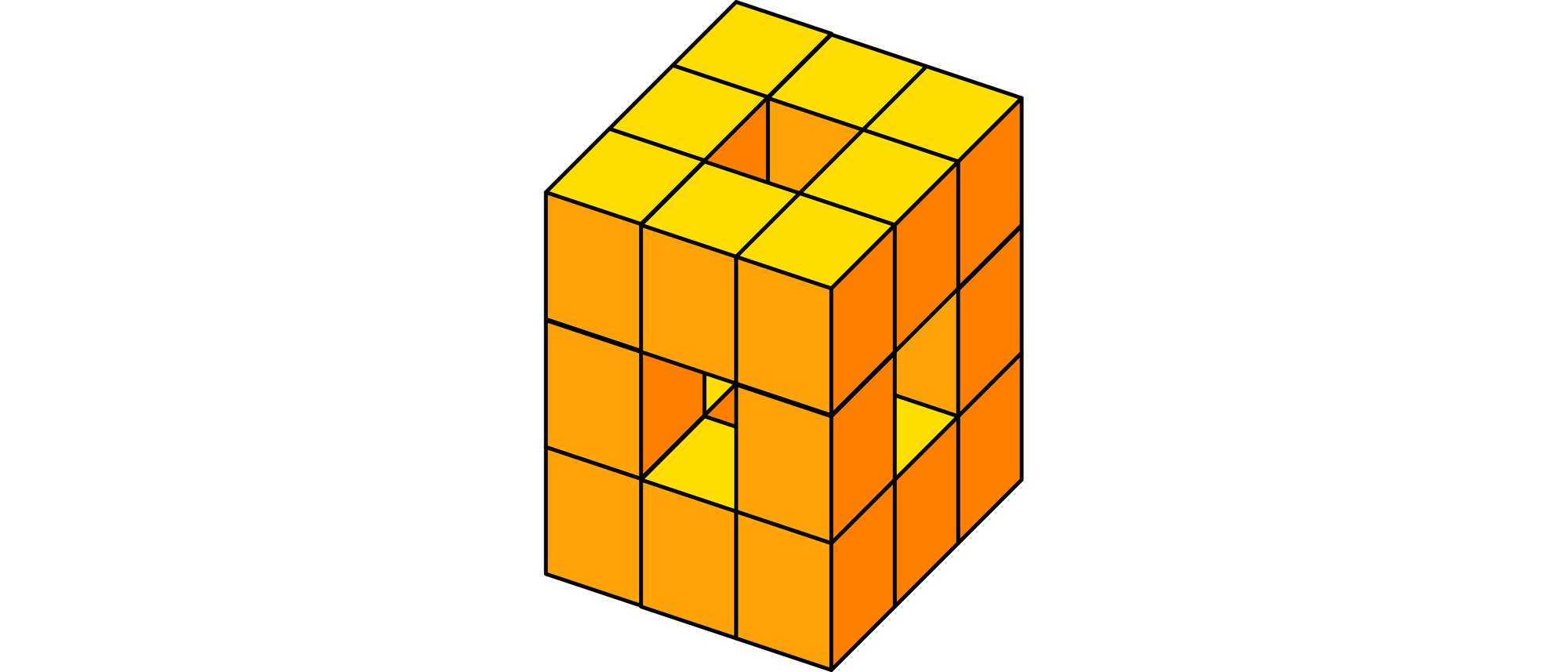
20 gleich große, gewöhnliche Spielwürfel, welche die Augenzahlen von 1 bis 6 tragen, sind zu einem würfelförmigen Gerüst, wie es die Skizze zeigt, zusammengeklebt worden. Dabei wurden immer nur Flächen mit gleicher Augenzahl aufeinander geleimt. Wie groß ist die Summe aller Augen auf den 72 freiliegenden Würfelflächen?
Wir bezeichnen die acht Spielwürfel an den Ecken des Würfelgerüsts als Eckwürfel und die zwölf dazwischen sitzenden als Kantenwürfel. Bei einem gewöhnlichen Spielwürfel ist die Summe der Augenzahlen auf zwei sich gegenüberliegenden Flächen immer 7.
Für diese Aufgabe bedeutet das, dass bei jedem der zwölf Kantenwürfel, bei denen jeweils zwei sich gegenüberliegende Seiten verleimt sind, immer sieben Augen verdeckt sind.
Jeder Kantenwürfel deckt auch an zwei Eckwürfeln jeweils eine Fläche ab. Da nur Flächen mit gleichen Augenzahlen aufeinander geleimt wurden, müssen diese beiden Eckwürfelflächen zusammen auch sieben Augen haben.
Weil 20 Würfel insgesamt 20 · (1 + 2 + 3 + 4 + 5 + 6) = 420 Augen haben, und 48 Flächen mit insgesamt 48 · 7/2 = 168 Augen abgedeckt sind, ist die Summe der sichtbaren Augen 420 − 168 = 252.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.