Hemmes mathematische Rätsel: Den wievielten Teil der Quadratfläche nimmt das gelbe Viereck ein?
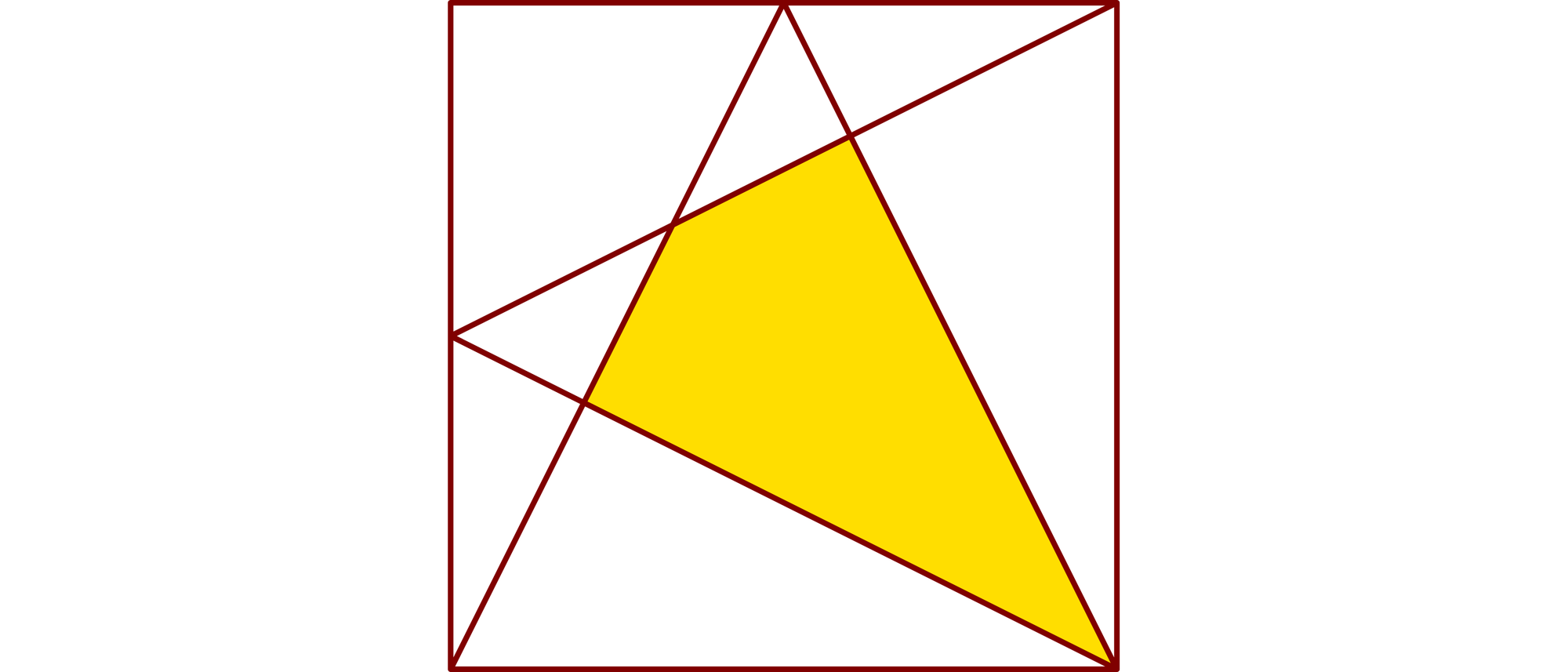
Der Mathematiklehrer Paul Eigenmann veröffentlichte 1981 das Buch »Geometrische Denkaufgaben«. In der Aufgabe 138 werden bei einem Quadrat drei Ecken mit den Mittelpunkten von zwei Seiten verbunden, so wie es die Zeichnung zeigt.
Durch die Verbindungslinien entsteht das gelbe Drachenviereck. Den wievielten Teil der Quadratfläche nimmt es ein?
Legt man über das große rote Quadrat ein Raster aus 3×3 kleineren blauen Quadraten, sieht man, dass die roten Linien im Inneren des roten Quadrates Diagonalen in blauen Doppelquadraten sind. Nun überzieht man noch jedes blaue Quadrat mit einem Raster aus 5×5 kleinen grünen Quadraten.
Da die roten Linien blaue Doppelquadrate diagonal durchlaufen, müssen sie es auch bei den kleinen grünen Doppelquadraten machen. Alle Schnittpunkte der roten Linien im Inneren des roten Quadrates liegen auf Punkten des grünen Rasters. Somit kann man das Problem durch Abzählen lösen: Das rote Quadrat besteht aus 152 = 225 grünen Quadraten und das gelbe Drachenviereck aus 60. Folglich nimmt der Drachen 60/225 = 4/15 der Quadratfläche ein.

Schreiben Sie uns!
Beitrag schreiben