Hemmes mathematische Rätsel: Der wievielte Teil des Ringes ist orange?
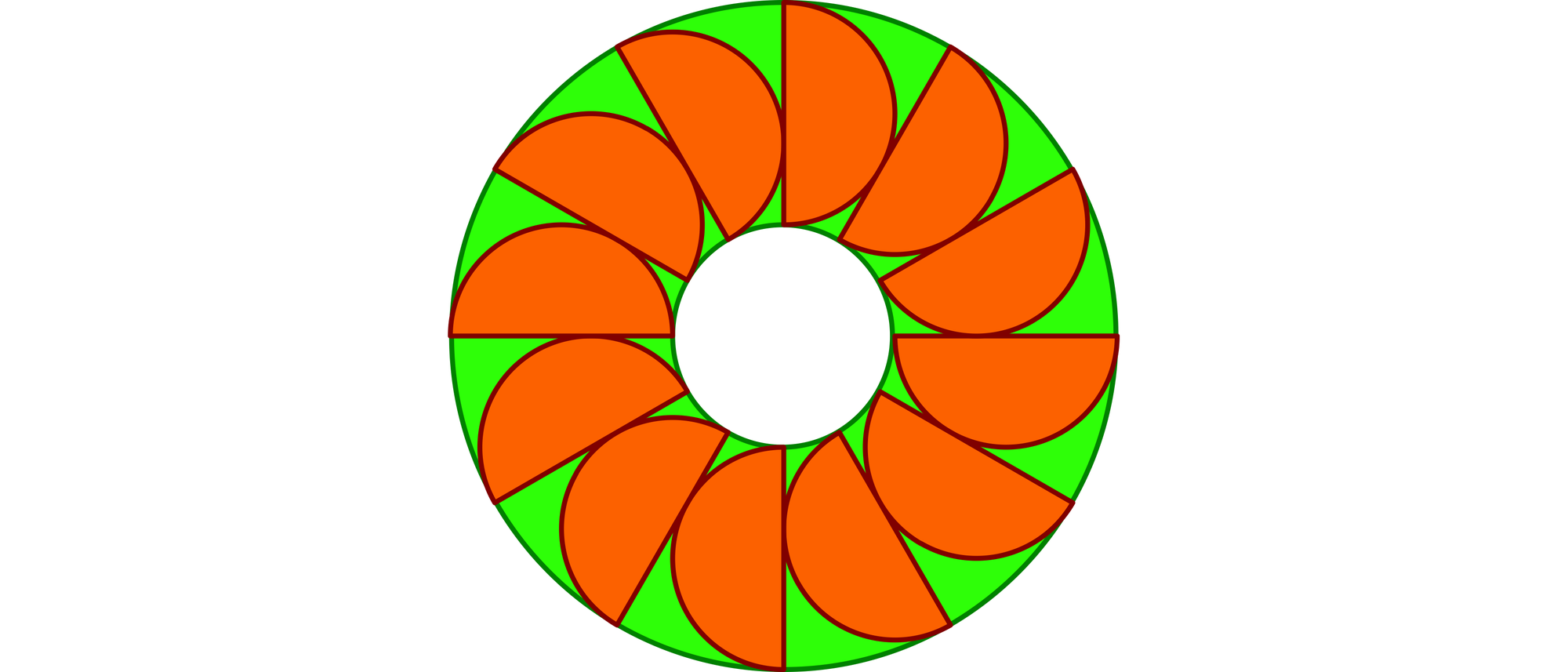
In einem Kreisring liegen zwölf gleiche Halbkreise. Ihre Durchmesser fallen alle auf Radien des Ringes. Der wievielte Teil des Ringes ist orange?
Wegen der Symmetrie des Ringes reicht es aus, nur ein Zwölftel von ihm zu betrachten. B ist der Mittelpunkt des Halbkreises und die Strecke AC eine Tangente an ihn. Folglich ist BA ein Radius r des Halbkreises. Der Winkel ACB ist 30° groß. Damit ist das rechtwinklige Dreieck ABC ein halbiertes gleichseitiges Dreieck, und BC hat die Länge 2r. Folglich hat der Ring den Innenradius r und der Außenradius 3r.
Seine Fläche beträgt darum π(3r)2 − πr2 = 8πr2. Die zwölf Halbkreise haben einen Inhalt von 12 · πr2/2 = 6πr2. Folglich ist 1 − 6πr2/(8πr2) = 1/4 des Ringes grün und somit 3/4 orange.
Anmerkung:
In der ursprünglichen Lösung befand sich ein Fehler, wonach bloß 1/4 der Fläche orange wäre.
Schreiben Sie uns!
5 Beiträge anzeigen