Hemmes mathematische Rätsel: Die Dreiecke auf den Parallelen
Mathematische Denksportaufgaben sind so alt wie die Mathematik selbst. Die ältesten überlieferten Rätsel sind mehrere Jahrtausende alt und stammen aus dem Zweistromland und Ägypten. Mathematische Rätsel kennt man in allen Kulturen und Staaten. Hier ist eine Aufgabe aus Bulgarien, die vor einiger Zeit in der Zeitschrift »Matematica«, die sich an Schüler, Studenten und Lehrer wendet, gestellt wurde.
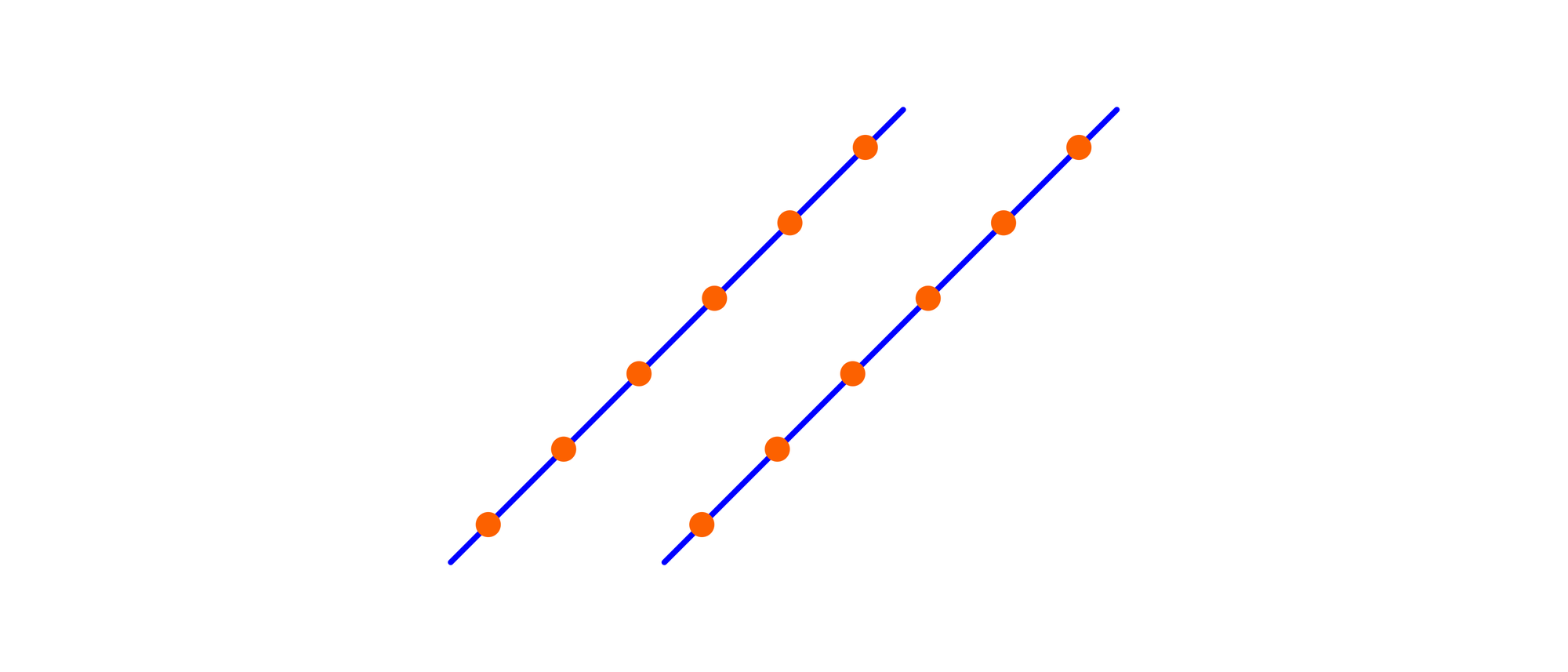
Auf zwei parallelen Linien liegen je sechs Punkte. Wie viele verschiedene Dreiecke gibt es, bei denen jeweils alle drei Ecken zu diesen zwölf Punkten gehören?
Wenn zwei Ecken des Dreiecks auf der linken Geraden liegen, so stehen für die erste Ecke sechs Punkte zur Auswahl. Für die zweite Ecke bleiben dann noch nur noch fünf Möglichkeiten übrig. Insgesamt sind dies also 6 · 5 = 30 verschiedene Punktpaare. Da aber die Reihenfolge der beiden Punkte bei den Ecken des Dreiecks keine Rolle spielt, sind es tatsächlich nur halb so viele, also 15 verschiedene Punktpaare.
Die dritte Ecke des Dreiecks muss auf der anderen Geraden liegen, denn sonst ergäben die drei Punkte kein Dreieck. Für sie gibt es also sechs Möglichkeiten. Damit kommen wir auf 15 · 6 = 90 Dreiecke.
Nun ist es aber auch möglich, dass nur eine Ecke auf der linken Geraden liegt und die beiden anderen sich auf der rechten Geraden befinden. Auch in diesem Fall sind 90 Dreiecke möglich, so dass die zwölf Punkte insgesamt 180 verschiedene Dreiecke bilden können.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.