Hemmes mathematische Rätsel: Die unsichtbare Kurve
1970 gründeten die beiden bekannten russischen Wissenschaftler A. N. Kolmogorov und I. K. Kikoyin die Zeitschrift »Kvant«, in der von Fachautoren auf anschauliche Weise über aktuelle Themen der Mathematik und der Physik für ein breites Publikum geschrieben wird. Die Zeitschrift wurde ein so großer Erfolg, dass ab 1990 auch eine amerikanische Ausgabe mit dem Titel »Quantum« erschien, die neben Übersetzungen aus der russischen Ausgabe auch Originalartikel publizierte. Leider blieb der amerikanischen Ausgabe der Erfolg der russischen versagt, so dass sie nach elf Jahren wieder eingestellt wurde. In Quantum erschienen auch zahlreiche Rätsel, wie beispielsweise 1995 das folgende von V. Proizvolov:
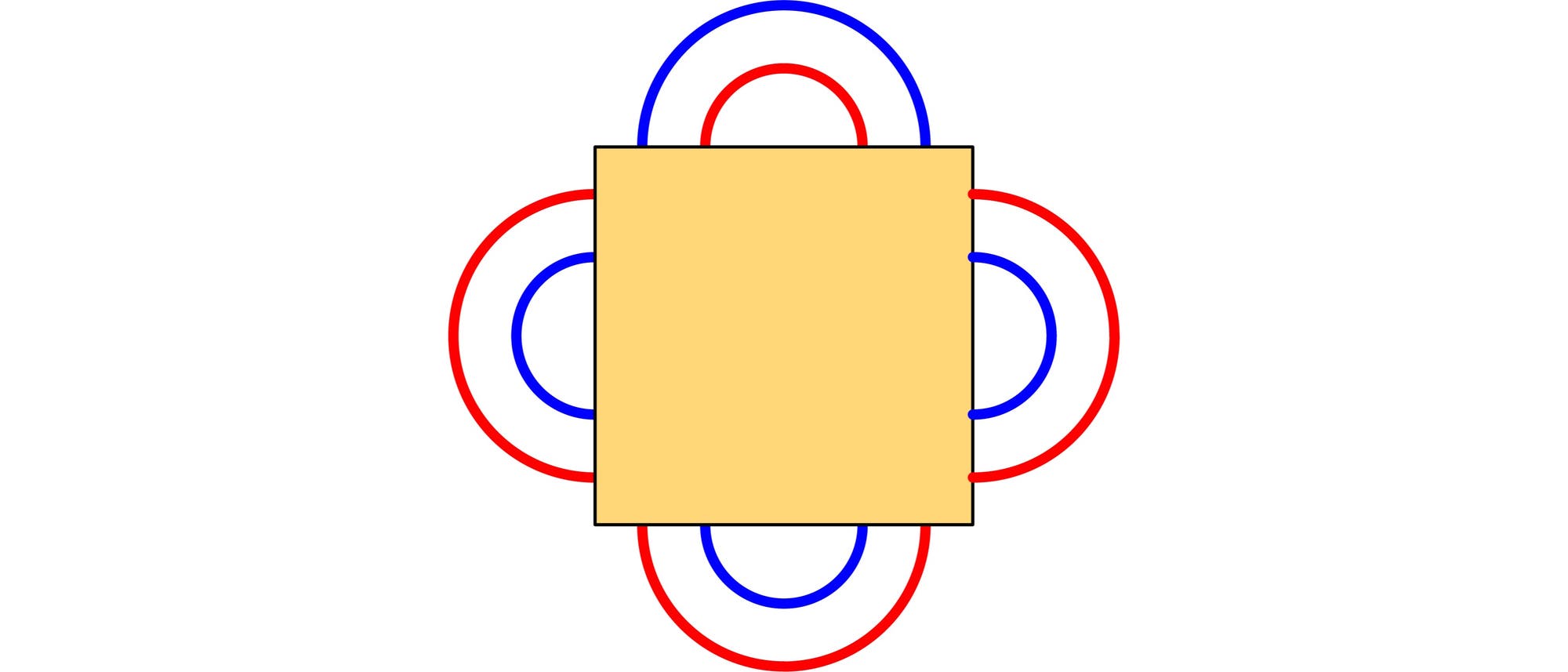
Auf einem Blatt Papier sind sechs geschlossene Kurven (ohne einen Anfang und ohne ein Ende), die sich nicht selbst und nicht gegenseitig schneiden. Drei dieser Kurven sind blau und die anderen drei sind rot. Ein Quadrat deckt fünf Kurven teilweise und eine Kurve vollständig ab. Welche Farbe hat die vollständig abgedeckte Kurve?
Der obere blaue Bogen kann mit keinen der drei anderen blauen Bögen zu einer geschlossenen Kurve verbunden sein, denn sonst kann der roten Bogen, der den betroffenen blauen Bogen umschließt, nicht mehr zu einer geschlossenen Kurve erweitert werden.
Wenn die drei kleinen blauen Bögen Teile einer einzigen geschlossenen blauen Kurve sind, müssen auch die drei großen roten Bögen zu einer einzigen geschlossenen roten Kurve gehören. Zusammen mit den beiden oberen Bögen und einer vollständig abgedeckten Kurve ergeben sie fünf geschlossene Kurven. Es müssen allerdings sechs sein. Also können die drei kleinen blauen Bögen nicht Teile einer einzigen geschlossenen blauen Kurve sein.
Also gehören die drei kleinen blauen Bögen zu zwei geschlossenen blauen Kurven und der große blaue Bogen gehört zur dritten geschlossenen blauen Kurve. Daraus folgt, dass die drei großen roten Bögen Teile einer einzigen geschlossenen roten Kurve sind und die vollständig abgedeckte Kurve auch rot sein muss.
Schreiben Sie uns!
Beitrag schreiben