Hemmes mathematische Rätsel: Die wunderbare Holzvermehrung
Gottfried Igelmund aus Vossenack in der Eifel stellte 2008 den Lesern der Aachener Nachrichten und der Aachener Volkszeitung eine verblüffende Rechnung vor:
Der Festmeter (fm) ist ein Raummaß für Holz und entspricht einem Kubikmeter fester Holzmasse ohne Zwischenräume. In der Forstwirtschaft wird der Festmeter-Inhalt eines Baumstamms mit der Formel πr2L berechnet. Dabei ist L die Länge des Stamms und r der Radius der Stammmitte.
Ein ideal gewachsener Fichtenstamm von 30 m Länge hat einen Kopfdurchmesser (dickes Ende) von 48 cm und einen Zopfdurchmesser (dünnes Ende) von 8 cm. Somit hat die Stammmitte einen Durchmesser von (48 + 8)/2 = 28 cm und einen Radius von r = 14 cm. Der Stamm enthält also π · 0,142 · 30 ≈ 1,85 fm Holz.
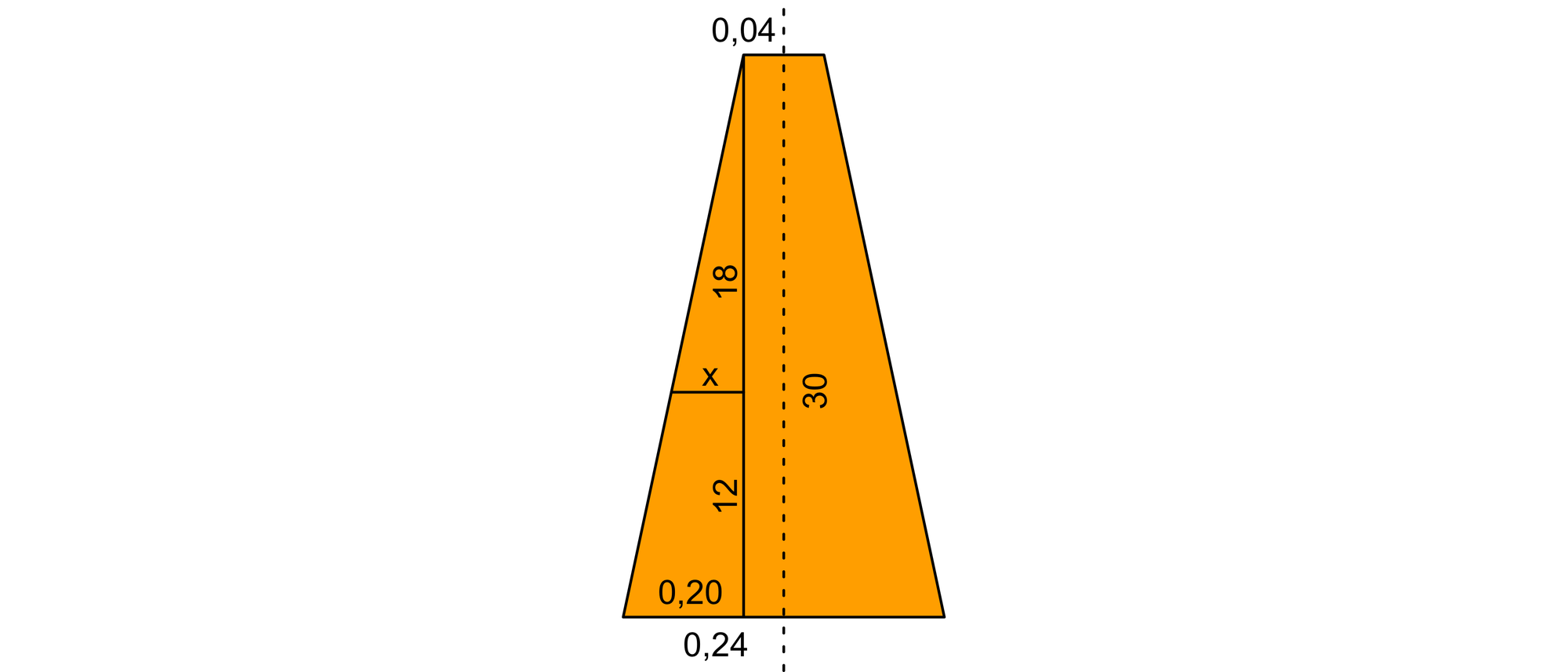
Nun wird der Stamm auf 24 m Länge gekürzt und das kurze dünne Ende weggeworfen. Für die Mitte des gekürzten Stammes gilt nach dem Strahlensatz x/18 = 0,20/30 oder x = 0,12. Damit hat der gekürzte Stamm einen Mittenradius von r = 0,12 + 0,04 = 0,16 m und folglich eine Holzmenge von π · 0,162 · 24 ≈ 1,93 fm.
Der gekürzte Stamm enthält somit mehr Holz als der ungekürzte. Wie lässt sich dieser Widerspruch erklären?
Natürlich enthält der gekürzte Stamm nicht mehr Holz als der ungekürzte. Der Fehler ist dadurch entstanden, dass die Formel der Forstwirtschaft nur begrenzt zur Volumenberechnung von Baumstämmen geeignet ist.
Etwas genauer, wenn auch komplizierter, wäre es, einen Baumstamm als Kegelstumpf anzunehmen. Dann würde man sein Volumen mit der Gleichung 1⁄3π(r2 + rR + R2)L berechnen, wobei L die Stammlänge, r der Zopf- und R der Kopfradius wären.
Mit dieser Gleichung ergäbe sich für den ungekürzten Stamm eine Holzmenge von 2,16 fm und für den gekürzten von 2,09 fm, womit der Widerspruch beseitigt wäre.
Schreiben Sie uns!
Beitrag schreiben