Hemmes mathematische Rätsel: DIN-Quader
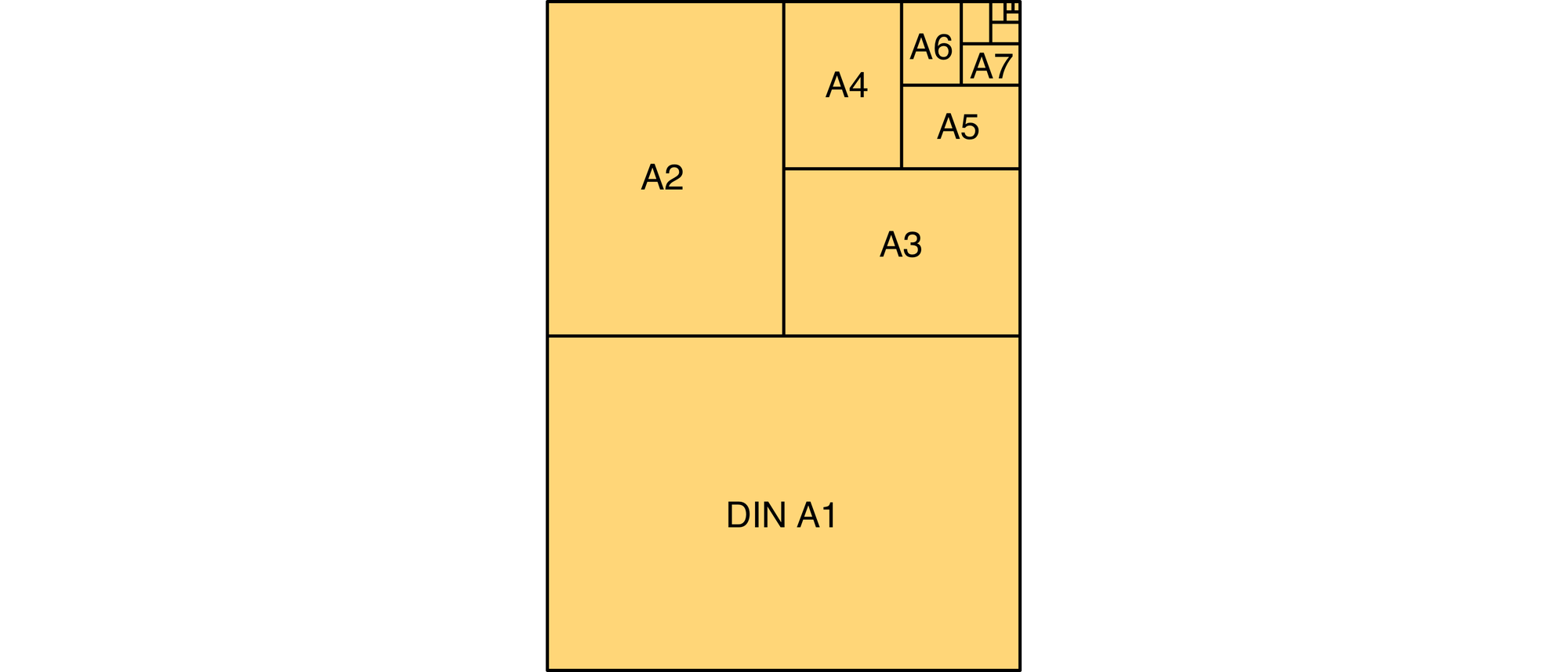
In der DIN-Norm 476 wurde 1922 festgelegt, dass das Grundmaß aller Papierformate ein rechteckiger Bogen von 1 m2 Größe ist, dessen Seitenlängen im Verhältnis 1 : √2 zueinander stehen. Sein Format wird als A0 bezeichnet. Halbiert man einen A0-Bogen parallel zu seinen kurzen Seiten, erhält man zwei A1-Bögen. Auch die Seiten des A1-Bogens stehen wieder im Verhältnis 1 : √2 zueinander. Dass das Seitenverhältnis genau 1 : √2 ist, hat einen guten Grund: Nur dann bleibt bei der Halbierung eines Bogens das Seitenverhältnis erhalten. Durch weitere Halbierungen erhält man die anderen A-Formate. Einen einzelnen A0-Bogen kann man also so zerschneiden, dass man je ein Blatt aller anderen Formate erhält. Diese Norm haben inzwischen, bis auf wenige Ausnahmen wie die USA oder Kanada, alle Staaten der Erde übernommen.
Ein DIN-K0-Quader ist ein Quader von 1m3 Volumen. Halbiert man ihn, entstehen zwei DIN-K1-Quader, deren Kanten im selben Verhältnis zueinander stehen wie die Kanten des DIN-K0-Quaders. Welche Kantenverhältnisse haben die DIN-Quader?
Die Kanten des DIN-K0-Quaders haben die Längen a, b und c, wobei a < b < c sein soll. Somit gilt für das Volumen des DIN-K0-Quaders abc = 1m3. Damit der DIN-K1-Quader, der nur ½ m3 groß ist, dieselben Kantenverhältnisse hat wie der DIN-K0-Quader, müssen alle seine Kanten um denselben Faktor x schrumpfen. Somit gilt für das Volumen des DIN-K1-Quaders xa • xb • xc = ½ m3, woraus x = 1 / 3√2 ≈ 0,7937 folgt.
Die längste Kante des K1-Quaders ist so lang wie die mittlere Kante des K0-Quader, was zu xc = b oder b : c = 1 : 3√2 führt. Die mittlere Kante des K1-Quaders ist so lang wie die kürzeste Kante des K0-Quaders, also xb = a oder a : b = 1 : 3√2. Die kürzeste Kante des K1-Quaders schließlich ist halb so lang wie die längste Kante des K0-Quaders, das heißt xa = c/2 oder a : c = 1 : 3√4.
Die Kantenlängen eines DIN-Quaders stehen also in den Verhältnissen a : b : c = 1 : 3√2 : 3√4 ≈ 1 : 1,2599 : 1,5874 zueinander.
Die Skizze zeigt eine maßstabsgerechte Abwicklung eines DIN-Quaders. Die Bezeichnungen DIN-K0- und DIN-K1-Quader sind übrigens keineswegs normiert, sondern nur für das Rätsel erfunden worden.
Schreiben Sie uns!
Beitrag schreiben