Dreiecke im Umkreissechseck
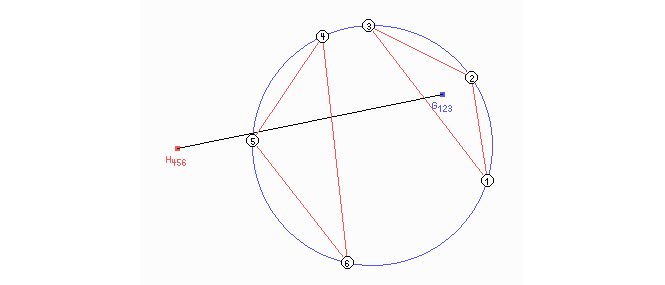
Die beiden Dreiecke haben einen gemeinsamen Umkreis. Eine Gerade verbindet den Schwerpunkt (\(G_{123}\)) des einen mit dem Höhenschnittpunkt (\(H_{456}\)) des anderen. Die sechs eingezeichneten Ecken lassen sich zu 20 Dreieckspaaren verbinden. Damit gibt es 20 solche Geraden. Wieso schneiden sie sich in einem gemeinsamen Punkt, und wo liegt dieser?
Euler-Gerade.
Das sieht schon ziemlich beachtlich aus, wie sich hier 20 Geraden, die von sechs zufälligen Punkten auf einem Kreis abstammen, in einem Punkt treffen!
Bekanntlich wird die Strecke (Euler-Gerade) zwischen Umkreismitte und Höhenschnittpunkt eines jeden Dreiecks von dessen Schwerpunkt im Verhältnis 1/3 zu 2/3 geteilt. Vom Umkreismittelpunkt geht man also zum Höhenschnittpunkt, indem man den Weg zum Schwerpunkt auf das Dreifache in gleicher Richtung verlängert (siehe auch "Coolidge").
Mit Schwerpunkt ist hier der Schwerpunkt von drei gleich schweren Gegenständen in den Ecken des Dreiecks gemeint, er ist zugleich auch der Schwerpunkt der Dreiecksfläche (aber nicht der der Kanten!).
Man kann die sechs Punkte auf 20 Arten als Ecken auf zwei Dreiecke aufteilen. Der Schwerpunkt \(G\) aller sechs Punkte ist dabei stets die Mitte zwischen den Schwerpunkten von zwei zu einem Paar gehörenden Dreiecken. Dazu müssen die sechs Punkte nicht einmal auf einem Kreis liegen. Wenn sie es aber doch tun, kann man vom gemeinsamen Umkreismittelpunkt \(U\) aller Dreiecke aus die Entfernungen zu den Schwerpunkten der einzelnen Dreiecke verdreifachen und zu deren Höhenschnittpunkten gelangen (zentrische Streckung um den Faktor 3). Zu dem Gesamtschwerpunkt \(G\) gehört auf diese Weise ein Punkt \(H\).
Dieser Punkt \(H\) ist nun wegen dieser Streckungs-Symmetrie der Mittelpunkt der Höhenschnittpunkte eines jeden der 20 Paare von Dreiecken, also auch der Schnittpunkt der 20 entsprechenden gelben Linien.
Betrachten wir nun ein Paar von Dreiecken, zum Beispiel mit den Ecken 1 2 3 und 4 5 6. Die beiden Schwerpunkte und die beiden Höhenschnittpunkte bilden das Trapez (\(G_{123}H_{123}H_{456}G_{456}\)). Dessen beide zueinander parallelen Grundseiten (pink) haben das Längenverhältnis 1:3, und ihre Mitten sind \(G\) und \(H\). Wie man ebenfalls leicht überlegen kann, teilt der Schnittpunkt der Diagonalen eines (jeden) Trapezes die Verbindungsstrecke zwischen den Mitten der Grundseiten im Verhältnis von der Längen dieser Grundseiten. Somit liegt dieser Schnittpunkt \(C\) in der Mitte zwischen \(U\) und \(H\), also vom gemeinsamen Umkreismittelpunkt \(U\) aus in 1,5-facher Verlängerung des Gesamtschwerpunktes \(G\). Da \(U\) und \(G\) für alle Dreiecke an gleicher Stelle liegen, tut es dieser Schnittpunkt \(C\) auch.
Schreiben Sie uns!
Beitrag schreiben