Hemmes mathematische Rätsel: Dreieckige und sechseckige Kacheln
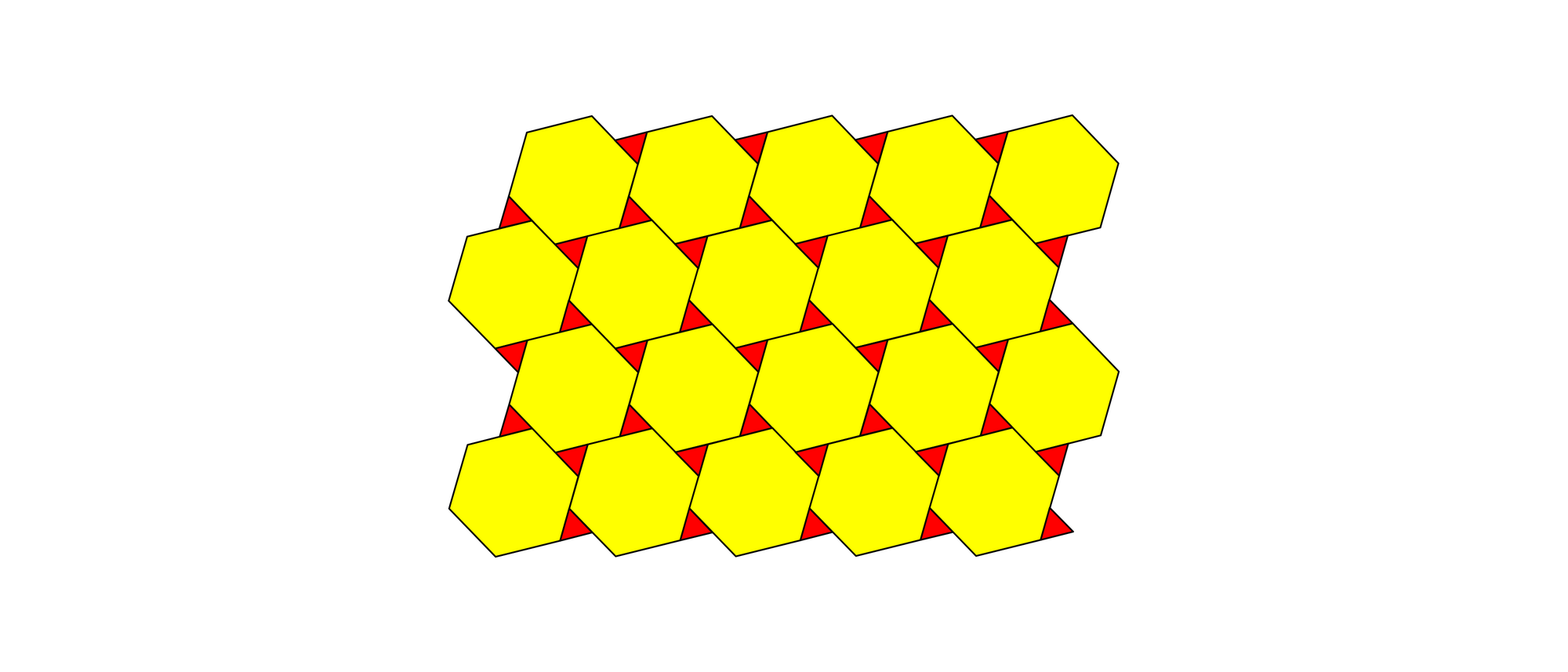
Bienen überdecken seit Urzeiten eine Ebene mit lauter gleichen regelmäßigen Sechsecken, während sie ihre Waben bauen. Jeder Fliesenleger weiß, dass dies auch mit lauter gleichen Quadraten oder gleichseitigen Dreiecken möglich ist. Weniger bekannt hingegen ist: Auch mit einer Mischung aus gleichseitigen Dreiecken und regelmäßigen Sechsecken kann man einen Boden lückenlos kacheln.
Der »United Kingdom Mathematics Trust« (UKMT) ist eine Organisation, die die Mathematikausbildung britischer Kinder unterstützt. Der UKMT wurde 1996 gegründet und organisiert eine Reihe von Mathematikwettbewerben. Darunter ist auch die »Intermediate Mathematical Challenge«, die bereits 1987 von dem englischen Mathematiker Tony Gardiner (* 1947) ins Leben gerufen wurde. Eine der Aufgaben dieses Wettbewerbs aus dem Jahr 2016 handelt von der Kachelung mit Dreiecken und Sechsecken. Wenn sich der Boden in alle Richtungen unendlich weit ausdehnt und die Seiten der gelben sechseckigen Kacheln doppelt so lang sind wie die der roten dreieckigen Kacheln, der wievielte Teil der Bodenfläche ist dann rot?
Fasst man überall zwei dreieckige rote Kacheln und eine sechseckige gelbe Kachel zu einer achteckigen rosa Kachel zusammen, sieht man, dass sich mit diesen neuen Kacheln auch der gesamte Boden lückenlos bedecken lässt. Um den roten Anteil vom Boden zu bestimmen, reicht es darum aus, ihn vom Achteck zu berechnen.
Jedes gelbe Sechseck lässt sich in 24 Dreiecke zerlegen, von denen jedes die Größe eines roten Dreiecks hat. Ein rosa Achteck setzt sich also aus 26 Dreiecken zusammen, von denen 2 rot und 24 gelb sind. 2/26 oder 1/13 jedes Achtecks und damit des gesamten Bodens sind folglich rot.
Schreiben Sie uns!
Beitrag schreiben