Ein Parallelogramm aus doppeltem Viereck
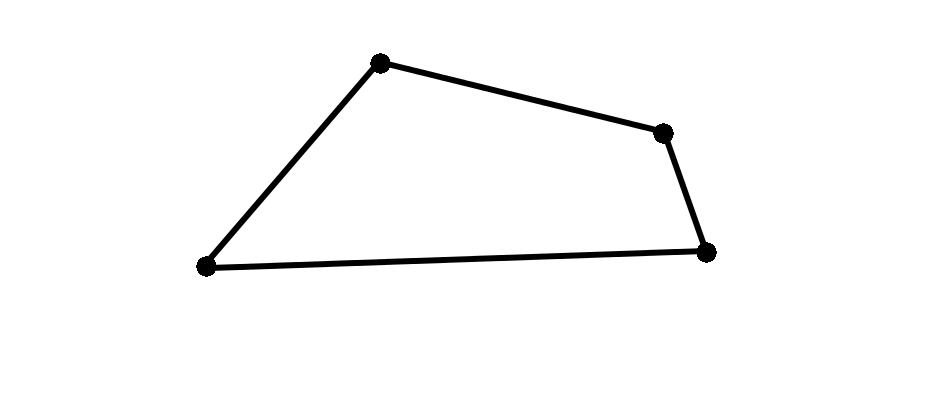
Zeigen Sie bitte: Aus zwei deckungsgleichen konvexen Vierecken kann man ein Parallelogramm legen, indem man die beiden Vierecke jeweils entlang einer Diagonalen teilt.
Legen Sie die beiden deckungsgleichen Vierecke in die Punktsymmetrie-Position bezüglich einer Seitenmitte.
Das ursprüngliche Viereck ist hier kräftig rot und blau gefärbt, orange und dunkelgrün ist sein deckungsgleiches Punkt-Spiegelbild (das ursprüngliche Viereck ist also nicht umgeklappt, sondern um 180 Grad um den Mittelpunkt seiner "Unterkante" gedreht worden). Verschiebt man das dunkelgrüne Dreieck in die hellgrüne Position und das dunkelblaue in die hellblaue, so bekommt man das gewünschte Parallelogramm, dessen Seiten die Diagonalen des gegebenen Vierecks sind.
Schreiben Sie uns!
Beitrag schreiben