Hemmes mathematische Rätsel: Ein unregelmäßiges Sechseck
Das populärwissenschaftliche britische Magazin »New Scientist« erscheint seit 1956 jede Woche. Von 1967 bis 1977 enthielt es die Kolumne »Tantalizer« (= Peiniger) mit mathematischen und logischen Rätseln, die von den »Puzzles« abgelöst wurde und 1979 in die Kolumne »Enigma« (= Rätsel) überging, bis sie Ende 2013 eingestellt wurde. Am 26. Januar 2002 stellte Richard England den Lesern das folgende Rätsel:
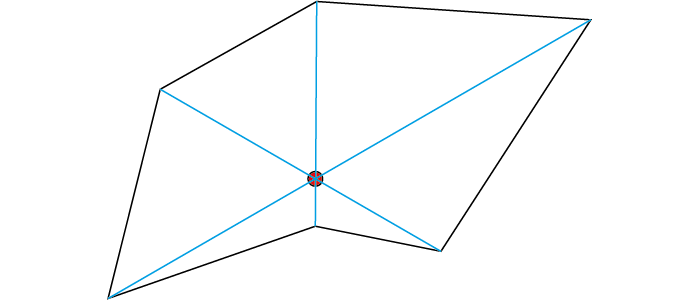
Ein unregelmäßiges Sechseck hat ganzzahlige Seitenlängen. Ein Punkt P im Inneren des Sechsecks wird durch Strecken mit den Ecken des Sechsecks verbunden und unterteilt es in sechs Dreiecke, die alle am Punkt P einen Innenwinkel von 60° haben. Die Längen dieser sechs Strecken sind unterschiedliche ganze Zahlen, von denen die kleinste eine 5 ist und die größte kleiner als 50 ist. Wie groß ist der Umfang des Sechsecks?
Treffen am Punkt P die beiden Dreieckseiten a und b unter einem Winkel von 60° zusammen, gilt nach den Kosinussatz für die dritte Seite c2 = a2 + b2 − 2ab cos 60°. Da cos 60° = 1/2 ist, vereinfacht sich die Gleichung zu c2 = a2 + b2 − ab.
Der kleinste Wert für a ist 5. Nun gilt es zwei ganzzahlige Werte für b zu finden, die kleiner sind als 50 und die zu ganzzahligen Werten von c führen. Dies ist etwas mühsam, aber mit einem Taschenrechner leicht zu bewältigen, und man erhält die zwei Zahlentripel (a, b, c) = (5, 8, 7) und (5, 21, 19).
Danach muss man Dreiecke finden, die an diese beiden Dreiecke schließen. Man muss also für a = 8 und a = 21 die passenden Werte für b suchen. Für den ersten Fall gibt es nur das Tripel (8, 15, 13), für den zweiten Fall sind es aber die zwei Tripel (21, 16, 19) und (21, 45, 39).
Von diesen Dreiecken ausgehend hangelt man sich weiter. Dabei wird man feststellen, dass es nur eine einzige Möglichkeit gibt, sechs Dreiecke unter den geforderten Bedingungen zu einem Sechseck anzuordnen. (Das Spiegelbild davon wird nicht als verschieden gesehen.) Der gesuchte Umfang des Sechsecks beträgt somit 138.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.