Gelenkpolygon mit maximaler Fläche
Bekanntlich hat der Kreis eine größere Fläche als jede andere geschlossene Linie mit dem gleichen Umfang.
Zeigen Sie nun bitte daraus, dass ein ebenes Polygon mit vorgegebenen Seitenlängen den maximalen Flächeninhalt hat, wenn die Ecken auf einem Kreis liegen.
Betrachten Sie die Kreissegmente zwischen zwei benachbarten Ecken eines konvexen Polygons (konkave Vielecke fallen natürlich sofort aus der Suche heraus).
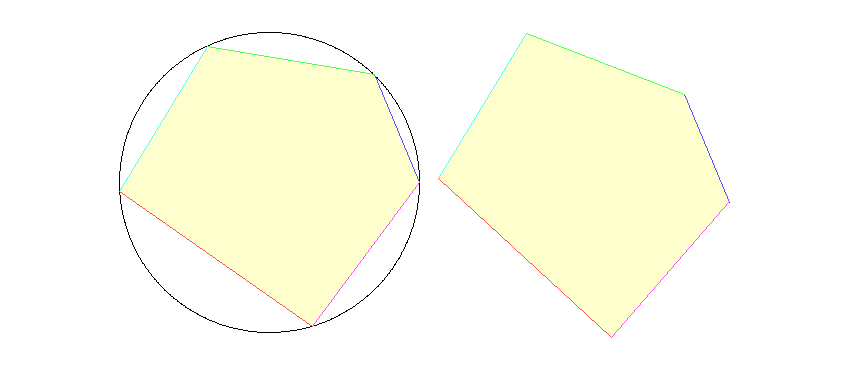
Nehmen Sie ein konvexes Polygon mit Ecken auf einem Kreis (links) und heften Sie gedanklich jedes Kreissegment zwischen zwei Ecken an seine zugehörige Seite. Dann deformieren Sie das Polygon mitsamt Kreissegmenten unter Erhaltung der Seitenlängen (stellen Sie sich die Seiten als Bleche aus dem Metallbaukasten vor, die an den Enden lose miteinander verschraubt sind). Die entstehende Figur (rechts) hat offensichtlich denselben Umfang wie der Kreis, aber wegen der Extremaleigenschaft des Kreises eine kleinere Fläche. Für das Innere des Polygons bleibt also auch weniger Fläche übrig. Schön einfach, nicht?
Schreiben Sie uns!
Beitrag schreiben