Hemmes mathematische Rätsel: Gesunde und kranke Quadrate
Der 1943 in Budapest geborene ungarisch-britische Mathematiker Béla Bollobás hat 2006 eine Sammlung mathematischer Denksportaufgaben mit dem Titel »The Art of Mathematics – Coffee Time in Memphis« veröffentlicht. Aus diesem Buch stammt das heutige Rätsel.
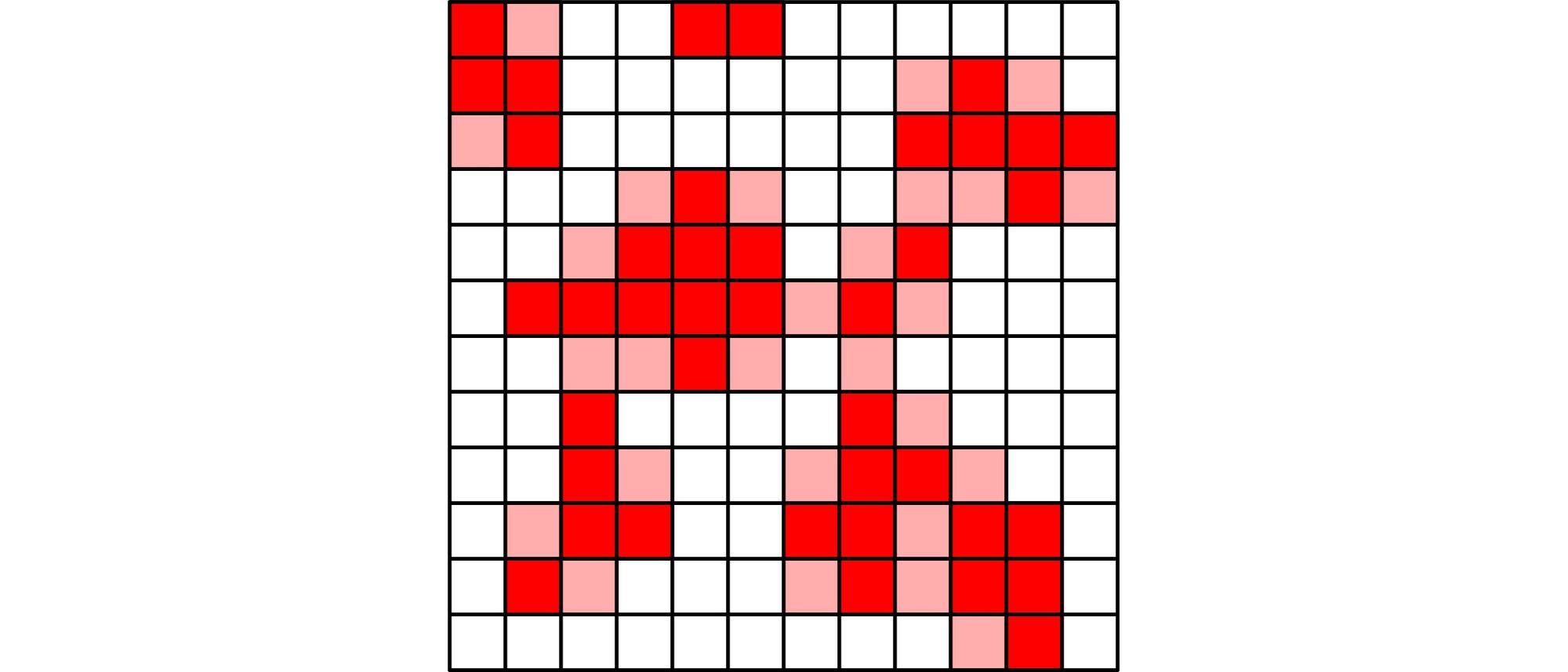
Auf einem Quadrat mit 12×12 Feldern sind einige Felder krank und rot markiert. Die Krankheit ist sehr ansteckend. Sind zwei oder mehr Nachbarfelder eines gesunden Feldes krank, infizieren sie das gesunde Feld. Dabei gelten nur Felder, die mit dem Feld eine gemeinsame Seite haben, als benachbart. Die infizierten Felder sind dann am nächsten Tag auch kranke Felder und können weitere Felder anstecken. In der Zeichnung, die nur ein Beispiel ist, sind die infizierten Felder rosa markiert. Wie viele Felder müssen zu Anfang mindestens krank sein, damit nach einigen Tagen alle Felder des Brettes krank sein können?
Die kranken roten Felder bilden mehrere Figuren auf dem Quadrat. Addiert man die Umfänge aller roten Figuren erhält man den Gesamtumfang des erkrankten Teils des Quadrats. Hat ein Feld eine Seitenlänge von einer Einheit, so beträgt in dem Beispiel der Gesamtumfang des erkrankten Teils 34 Einheiten.
Ein gesundes Feld, das sich durch genau zwei kranke Felder infiziert und keinen Kontakt zu anderen infizierten Felder hat, lässt der Gesamtumfang unverändert. Dies ist im Beispiel bei den Feldern A der Fall. In allen anderen Fällen verringert ein infiziertes Feld den Gesamtumfang um eine Einheit (Felder B), zwei Einheiten (Feld C) oder sogar vier Einheiten (Feld D). Wenn am Ende das ganze 12×12-feldige Quadrat krank ist, hat der Gesamtumfang der kranken Teile eine Länge von 48 Einheiten. Im günstigsten Fall hat sich der Gesamtumfang an keinem einzigen Tag verkleinert. Dann hatten die kranken Felder am ersten Tag auch einen Gesamtumfang von 48 Einheiten. Damit für diesen Gesamtumfang möglichst wenige Felder benötigt werden, sollten sie einzeln auf dem Quadrat liegen. Zwölf einzelne Felder reichen für einen Gesamtumfang von 48 Einheiten aus.
Dass auch zwölf Felder tatsächlich das ganze Quadrat infizieren können, sieht man leicht, wenn sie beispielsweise alle auf einer Diagonalen liegen. Am zweiten Tag sind dann auch die elf schräg darüber und die elf schräg darunterliegenden Felder krank, am dritten Tag auch die zehn darüber und die zehn darunter liegenden Felder. So geht das Tag für Tag weiter, bis schließlich am zwölften Tag alle Felder krank sind.
Schreiben Sie uns!
Beitrag schreiben