Gleiche Kreise im Dreieck
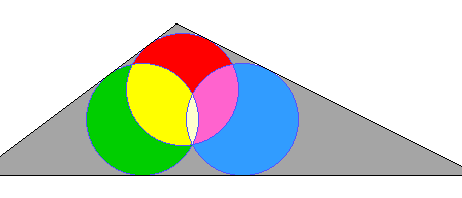
In ein beliebig vorgegebenes Dreieck sollen drei gleich große Kreise gezeichnet werden, die sich in einem Punkt schneiden. Außerdem soll jede Dreiecksseite von zwei dieser Kreise berührt werden.
Was für ein Dreieck bilden die Mittelpunkte dieser Kreise? Der (gemeinsame) Inkreismittelpunkt spielt eine wichtige Rolle als Ähnlichkeitszentrum.
Die Mittelpunkte der drei Kreise bilden ein Dreieck, das zu dem gegebenen ähnlich und parallel orientiert ist. Der Schnittpunkt der drei Kreise ist der Umkreismittelpunkt des kleinen Dreiecks. Dieser Umkreis hat den gleichen Radius wie die drei gesuchten Kreise.
Beide Dreiecke haben einen gemeinsamen Inkreismittelpunkt (warum?) und haben diesen als Ähnlichkeitszentrum (d. h. sie gehen durch zentrische Streckung bezüglich dieses Punktes auseinander hervor). Der Schnittpunkt liegt daher auf der geraden Verbindung von Inkreis- und Umkreismittelpunkt.
Das Streckungsverhältnis ist \(r_i / (r_i+r_u)\), da der Inkreisradius des großen Dreiecks so groß ist wie die Summe aus In- und Umkreisradius des kleinen.
Man bestimmt also zur Konstruktion erst die beiden Radien des gegebenen Dreiecks und daraus das genannte Streckungsverhältnis. Mit ihm findet man auf den Winkelhalbierenden vom Inkreismittelpunkt aus die Ecken des kleinen Dreiecks und damit die Mittelpunkte der gesuchten Kreise.
Schreiben Sie uns!
Beitrag schreiben