Hemmes mathematische Rätsel: In welchem Verhältnis müssen die beiden Radien zueinander stehen?
Der 1951 geborene Architekt Karl Flormann aus Bielefeld hat schon etliche Aufgaben zur Rätsel-Kolumne beigetragen. Das heutige Problem aus der ebenen Geometrie erhielt ich von ihm im März 2022.
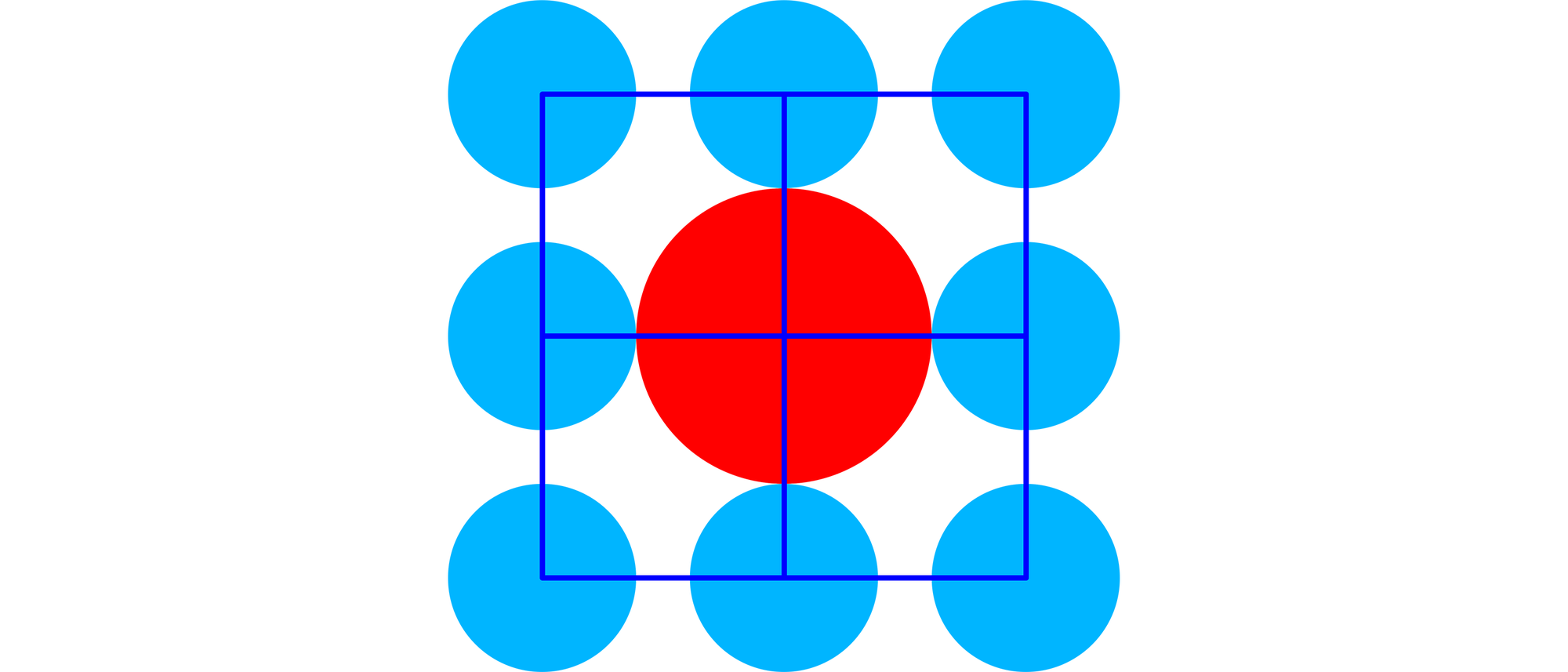
Auf den Ecken eines 2×2-feldigen quadratischen Rasters liegen die Mittelpunkte von acht blauen Kreisen und einem roten Kreis. Alle blauen Kreise sind gleich groß, und der rote Kreis ist so groß, dass er vier der blauen Kreise berührt. In welchem Verhältnis muss der Radius R des roten Kreises zum Radius r der blauen Kreise stehen, damit der rote Kreis alle acht blauen Kreise tangiert?
Der rote Kreis kann die acht blauen Kreise nur dann alle tangieren, wenn er so groß ist, dass die vier Eckkreise außerhalb und die vier anderen Kreise innerhalb seiner Fläche liegen. Haben die Quadrate des Rasters die Seitenlänge 1 und damit die Diagonalenlänge √2, so gilt R – r = 1 und R + r = √2. Dabei ist R der Radius des roten Kreises und r der Radius der blauen Kreise. Addiert man die beiden Gleichungen, erhält man 2R = √2 + 1, und subtrahiert man sie, bekommt man 2r = √2 – 1. Daraus folgt R/r = (√2 + 1)/(√2 – 1) = (√2 + 1)2 = 3 + 2√2 ≈ 5,83.
Schreiben Sie uns!
1 Beitrag anzeigen