Hemmes mathematische Rätsel: In welchem Verhältnis steht die lange zur kurzen Grundseite?
© Heinrich Hemme (Ausschnitt)
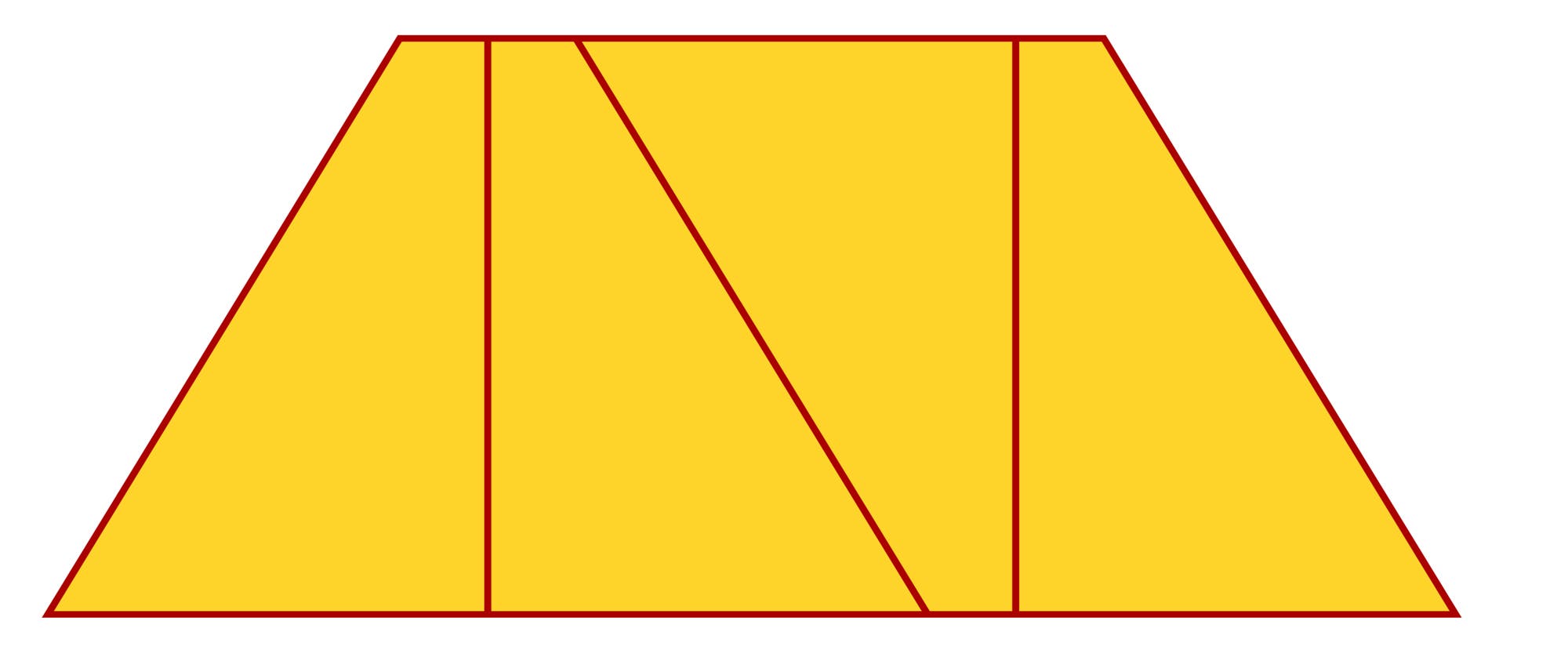
Ein gleichschenkliges Trapez, das die Form eines halben regelmäßigen Sechsecks hat, wird in vier kongruente rechtwinklige Trapeze zerlegt. In
Ein regelmäßiges Sechseck setzt sich aus sechs gleichseitigen Dreiecken zusammen.
© Heinrich Hemme (Ausschnitt)
Folglich ist die lange Grundseite des gleichschenkligen Trapezes doppelt so lang wie die kurze. Sind a und b die Längen der kurzen und der langen Grundseite der rechtwinkligen Trapeze, so gilt 2(3a + b) = a + 3b, was man zu b = 5a umformen kann. Die lange Grundseite ist also fünfmal so lang wie die kurze.
© Heinrich Hemme (Ausschnitt)
Hat Ihnen dieses Rätsel gefallen? Dann rätseln Sie doch einfach direkt weiter:
- Was ist die nächste Zahl in der Reihe?
- Wie groß ist x in diesen Dreiecken?
- Was ist die kleinste Zahl, die diesen Bedingungen gehorcht?
- Wie viele Dreiecke enthält diese Figur?
- Wie lang ist die Sehne des Kreises?
- Welche Zahl fehlt?
- Wie groß ist die Fläche des Halbkreises?
- Mit welcher Zahl muss die Reihe fortgesetzt werden?
- Wie viel deckt das Quadrat ab?
- Wie muss das Streichholz umgelegt werden?
- Wie viele Turmquadrate passen ins Schachbrett?
- Wie lang sind die Seiten des Quadrats?
Eine Übersicht über alle Matherätsel finden Sie unter https://www.spektrum.de/raetsel/. Viel Spaß beim Weiterknobeln!
Schreiben Sie uns!
Beitrag schreiben