Hemmes mathematische Rätsel: Welches Verhältnis haben die Seitenlängen?
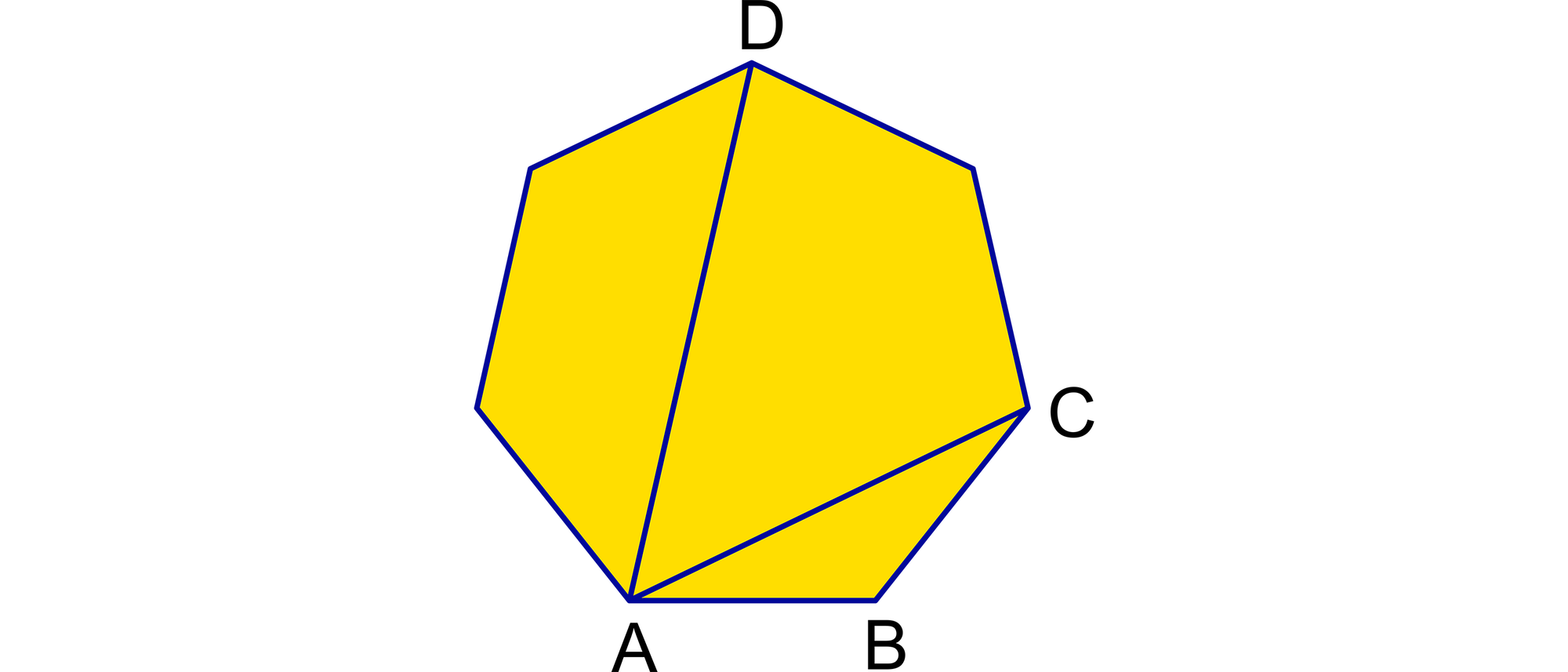
Die Strecken AB, AC und AD sind eine Seite und zwei unterschiedlich lange Diagonalen eines regelmäßigen Siebenecks. Ist der Kehrwert der Seitenlänge größer oder kleiner als die Summe der Kehrwerte der beiden Diagonalenlängen, oder sind beide Ausdrücke gleich groß?
Ein regelmäßiges Siebeneck besitzt, wie auch alle anderen regelmäßigen Vielecke, einen Umkreis. Folglich gilt für jedes Viereck, das man aus vier seiner Ecken bilden kann, der Satz des Ptolemäus: In einem Sehnenviereck ist das Produkt der Längen der Diagonalen gleich der Summe der Produkte der Längen sich gegenüberliegender Seiten. Wendet man diesen Satz auf das Viereck ACED an, erhält man AE ∙ CD = CE ∙ AD + ED ∙ AC. Da ED = CE = AB, AE = AD und da CD = AC ist, kann man die Ptolemäusgleichung auch als AD ∙ AC = AB ∙ AD + AB ∙ AC schreiben. Teilt man beide Seiten der Gleichung durch AB ∙ AC ∙ AD, vereinfacht sie sich zu 1/AB = 1/AC + 1/AD. Der Kehrwert der Seitenlänge ist folglich genauso groß wie die Summe der Kehrwerte der beiden Diagonalenlängen.
Schreiben Sie uns!
Beitrag schreiben