Inkreis und Umkreis beim Fünfeck
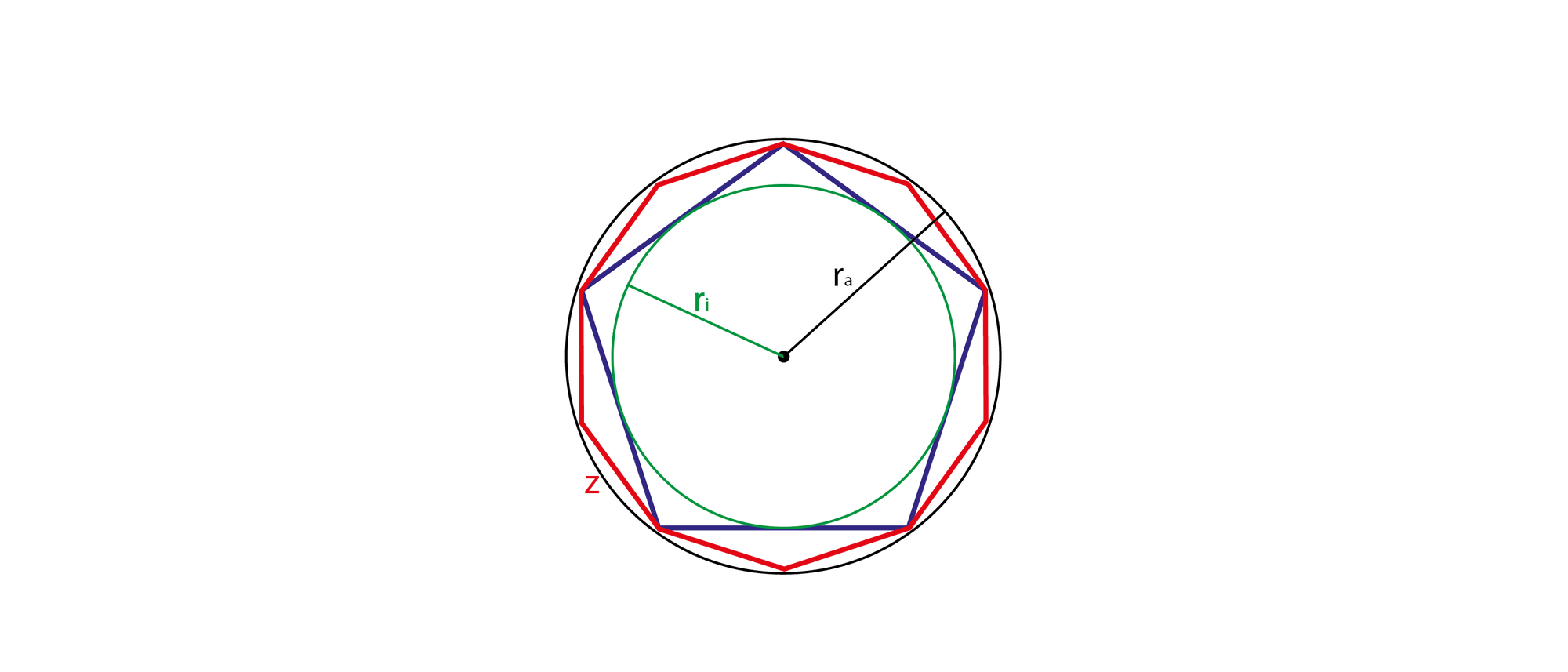
Können Sie folgende Aussage beweisen? Wenn \(r_a\) und \(r_i\) die Radien des Umkreises und des Inkreises eines regelmäßigen Fünfecks sind und \(z\) die Seite eines regelmäßigen Zehnecks mit dem gleichen Umkreis, so ist \(2 r_i = z + r_a\).
Die gelbe Raute hat eine Kantenlänge von \(r_a\), und ihre kurze Diagonale (rot) ist so lang wie eine Zehnecksseite \(z\) (verschieben Sie das Dreieck aus dieser Diagonale und einer der spitzen Ecken der gelben Raute so, dass die spitze Ecke in den Mittelpunkt zu liegen kommt). Die kleine orangefarbene Raute hat die Kantenlänge \(z\). Deren kurze Diagonale (blau) hat die Länge \(b=r_a-z\). Zugleich ist \(z+b/2=r_i\) (eine rote plus eine halbe blaue Rautendiagonale). Aus beiden Gleichungen zusammen folgt die Behauptung \(2r_i=r_a+z\).
Schreiben Sie uns!
Beitrag schreiben