Hemmes mathematische Rätsel: Können Sie die drei Dreiecke zu einem neuen zusammensetzen?
»Aus Eins mach’ Zehn, und Zwei lass gehn, und Drei mach’ gleich«, verlangte Johann Wolfgang von Goethe in seinem Hexeneinmaleins. Manfred Pietsch aus Kreuzau in Nordrhein-Westfalen war 2021 in den »Aachener Nachrichten« und in der »Aachener Zeitung« bescheidener und bat nur:
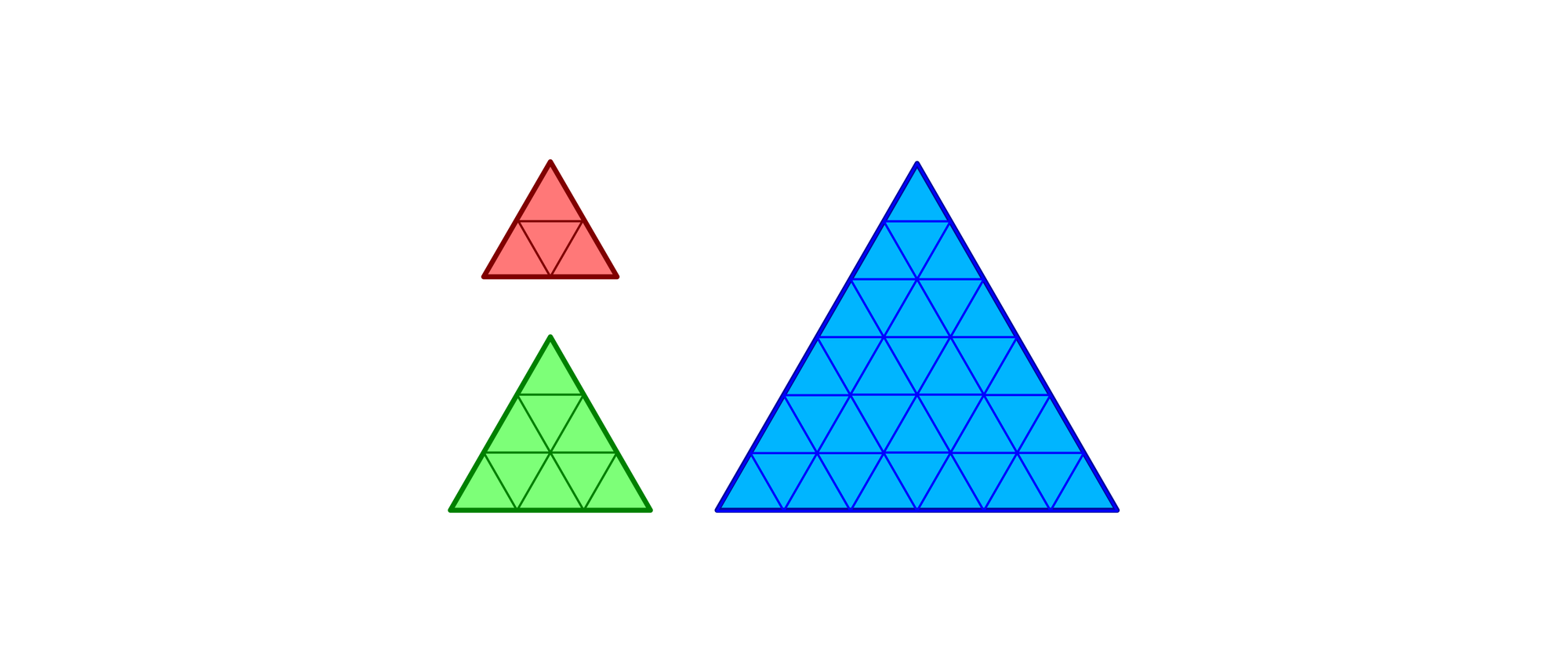
»Aus Drei mach Eins«: Zerschneiden Sie die drei gleichseitigen Dreiecke mit den Seitenlängen 2, 3 und 6 entlang der Feldgrenzen in fünf Teile und fügen Sie diese anschließend zu einem neuen und größeren gleichseitigen Dreieck wieder zusammen. Das neue Dreieck darf natürlich keine Lücken und keine Überlappungen haben.
Ist das Problem überhaupt lösbar?
Ein gleichseitiges Dreieck der Seitenlänge n besteht auch n2 kleinen gleichseitigen Dreiecken der Seitenlänge 1. Die drei gleichseitigen Dreiecke mit den Seitenlängen 2, 3 und 6 bestehen folglich aus 22 + 32 + 62 = 49 = 72 kleinen Dreiecken. Das neue gleichseitige Dreieck muss darum die Seitenlänge 7 haben.
Schreiben Sie uns!
Beitrag schreiben