Heute, am 14. März, wird wie jedes Jahr der Pi-Tag gefeiert; und das schon seit 1988. Der amerikanische Physiker Larry Shaw hatte die Idee, und sie hat inzwischen überall auf der Welt Anhänger gefunden. Zudem wurde der 14. März von der UNESCO zum »Internationalen Tag der Mathematik« erklärt und 2020 zum ersten Mal gefeiert.

Un das aus gutem Grund: Es gilt, die Bedeutsamkeit der Mathematik für die Erziehung und Bildung für Jung und Alt nicht aus dem Bewusstsein zu verlieren. Aber warum gerade der 14.. März? Die Antwort ist einfach. In den USA wird beim Schreiben des Datums der Monat zuerst genannt; aus 14.3. wird also 3/14. Der ungefähre Wert für die Zahl π ist 3,14. Traditionell wird an diesem Tag ein kreisrunder Kuchen gegessen, verziert mit Zuckerguss, der das Zeichen π oder auch die Zahlenfolge 3,14159 darstellt.

Ein idealer Zeitpunkt für das Anschneiden des Kuchens wäre aus meiner Sicht 9. Minuten nach 15. Uhr, denn π ≈ 3,14159. So erhalten die drei weiteren Dezimalstellen ihre besondere Deutung. Kreisrund sollte der Kuchen schon sein, weil ohne die Zahl π, auch Kreiszahl genannt, die Berechnung von Umfang und Flächeninhalt des Kreises nicht möglich wäre.

Besondere Rolle in der Geometrie

Die beiden Formeln lauten U = 2·rπ (Umfang) und A = π·r² (Flächeninhalt). Um die Formel für den Flächeninhalt zu verstehen, kann die folgende Erklärung helfen: Die Fläche des Kreises ist ungefähr dreimal so groß wie das Quadrat, dessen Seitenlänge so groß sein muss wie der Radius des Kreises. Und das Quadrat ist ja sehr leicht zu berechnen: A_Q = r² und der Kreis ist ungefähr 3·r².

Will man die Fläche des Kreises genau berechnen, muss die Zahl 3,14159... mit der Quadratfläche multipliziert werden. Da diese Zahl π aber niemals genau bestimmt werden kann, wird es auch keinen exakten Wert für den Flächeninhalt des Kreises geben. Daher auch der Spruch »Pi mal Daumen« für ungefähre Rechnungen, wenn es nicht so genau auf das Ergebnis ankommt.

Viele Mathematiker und Informatiker auf der ganzen Welt versuchen mit immer leistungsstärkeren Rechnern, weitere Stellen nach dem Komma für die irrationale Zahl Pi zu bestimmen – allerdings mit der Gewissheit, dass es niemals ein Ende geben kann (zurzeit liegt der Rekord bei mehr als einer Billionen Dezimalstellen). Tatsächlich lässt sich Pi auf die seltsamsten Arten berechnen, etwa durch die Anzahl von Stößen beim Billard – auch wenn diese Methode nicht wirklich effizient ist.

Jeder Geburtstag ist in Pi enthalten

Übrigens tauchen die Geburtstagsdaten eines jeden Menschen an irgendeiner Stelle der Zahl Pi auf. Wer also am 14.3. seinen Geburtstag feiert, ist ganz vorne mit dabei.

Wer einmal selbst einen Näherungswert für π bestimmen möchte, dem kann ich das folgende Experiment empfehlen: Man schneide aus Pappe einen Kreis mit dem Radius r = 8 cm aus (so exakt wie möglich). Aus der gleichen Pappe wird ein Quadrat mit der Seitenlänge 8 cm geschnitten. Nun müssen beide Teile mit einer sehr genauen Waage gewogen werden. Teilt man nun den erhaltenen Wert des Kreises durch den Wert des Quadrates ist das Ergebnis näherungsweise 3,14.

Übrigens: Einer der bedeutendsten Physiker der Neuzeit, Albert Einstein, wurde am 14.3. geboren (1879 in Ulm). Und im Jahr 2018 verstarb Stephen Hawking am 14.3., einer der führenden Physiker und Mathematiker der Gegenwart. Allein diese beiden hervorragenden Wissenschaftler hätten einen eigenen Gedenktag verdient.

Das Rätsel anlässlich des Pi-Tags

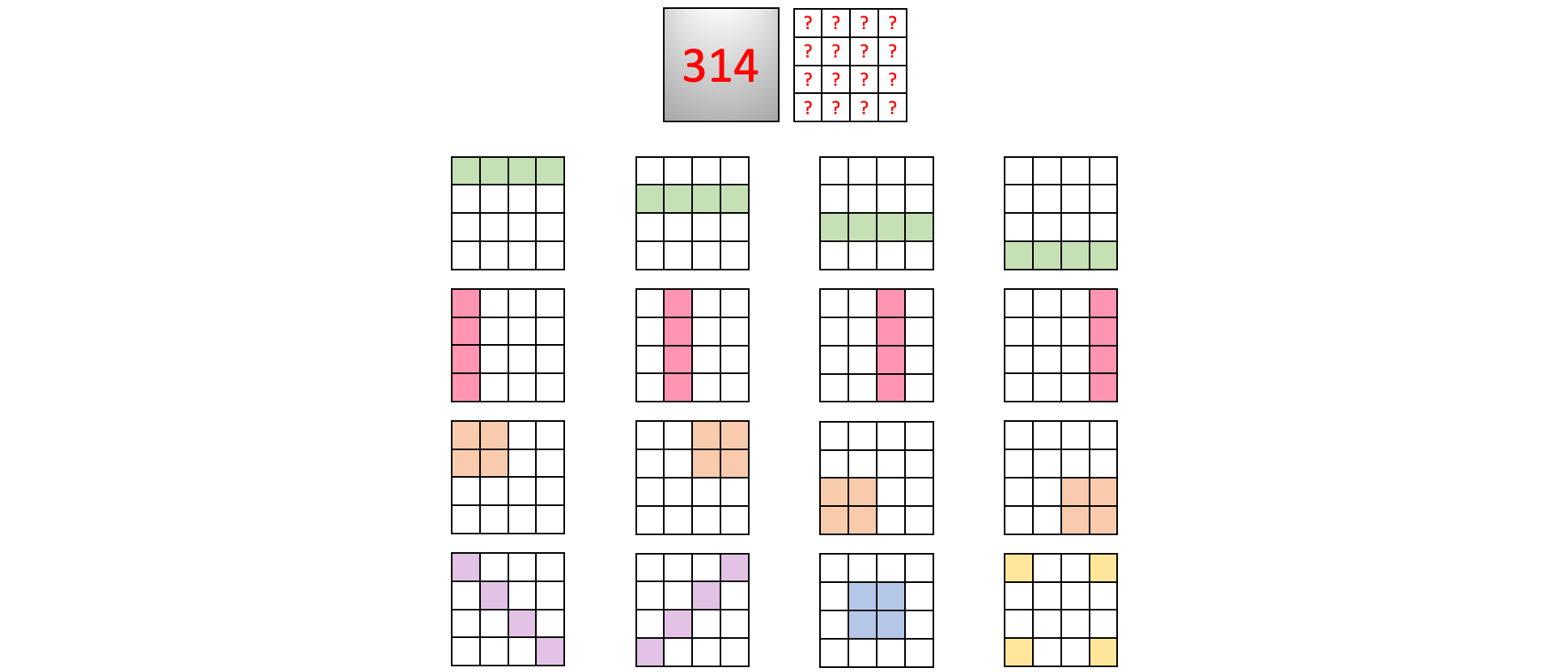
Verteilen Sie 16 verschiedene Zahlen so auf die 16 kleinen Quadrate, dass die Summe von vier Zahlen jeweils den Wert 314 hat.

Dies soll für alle gleichfarbigen Felder gelten, wie die Abbildung zeigt.