Hemmes mathematische Rätsel: Magische Kreise
Der chinesische Mathematiker Yang Hui, der während der Song-Dynastie lebte, wurde um 1238 geboren und starb um 1298. In seinem Buch »Xiangjie Jiuzhang Suanfa« aus dem Jahre 1261 findet man die älteste noch erhaltene chinesische Darstellung des Pascalschen Dreiecks. Er entdeckte es jedoch nicht selbst, sondern verweist darauf, das Dreieck von Jia Xian, der um 1050 lebte, übernommen zu haben. Dennoch wird das Pascalsche Dreieck noch heute in China als Yang-Hui-Dreieck bezeichnet. Um 1275 schrieb es das Buch »Xugu Zhaiqi Suanfa«, in dem er seine magischen Kreise vorstellt.
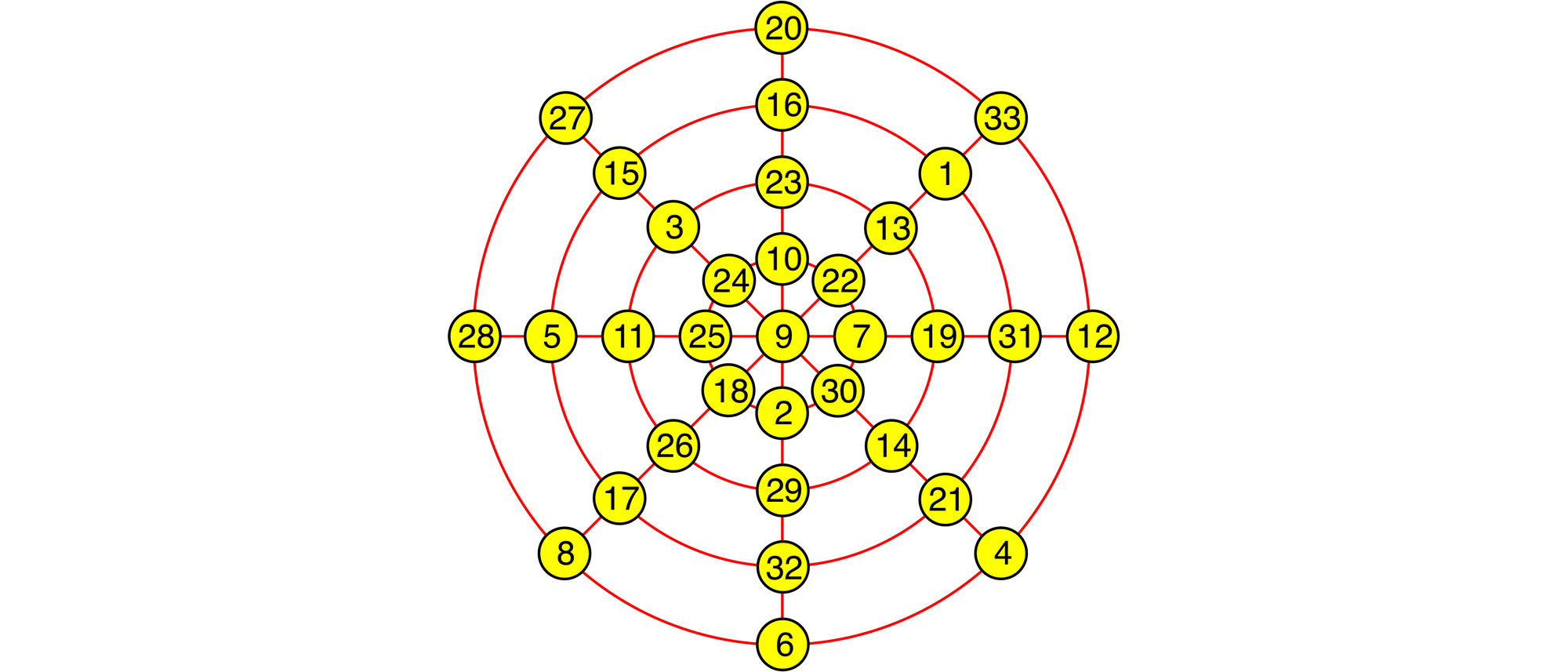
Yang Hui hat die Zahlen von 1 bis 33 so in die 33 gelben Felder des Musters gesetzt, dass die Summe der je acht Zahlen auf jedem der vier Kreise den Wert 138 ergibt und außerdem die Summe der je fünf Zahlen auf jedem der acht Radien einschließlich des Mittelfeldes den Wert 78 ergibt. Setzen Sie die Zahl 25 auf das Mittelfeld und verteilen Sie die restlichen Zahlen von 1 bis 33 so auf die noch freien Felder des Musters, dass die Summe der je acht Zahlen auf jedem der vier Kreise den Wert M ergibt und außerdem die Summe der je fünf Zahlen auf jedem der acht Radien einschließlich des Mittelfeldes den Wert N ergibt. Es gibt zahlreiche Lösungen dieser Aufgabe. Finden Sie eine davon.
Ersetzt man jede Zahl x, die Yang Hui in sein Diagramm geschrieben hat, durch die Zahl 34 − x, enthält das Diagramm anschließend wieder jede Zahl von 1 bis 33 und auf dem Mittelfeld steht, wie gefordert, die Zahl 25. Die Summe der Zahlen auf jedem der vier Kreise beträgt M = 8 · 34 − 138 = 134 und auf jeden der acht Radien N = 5 · 34 − 78 = 92.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.