Rätseln mit Eder: 13 Zahlen, vier Quadrate, ein Problem
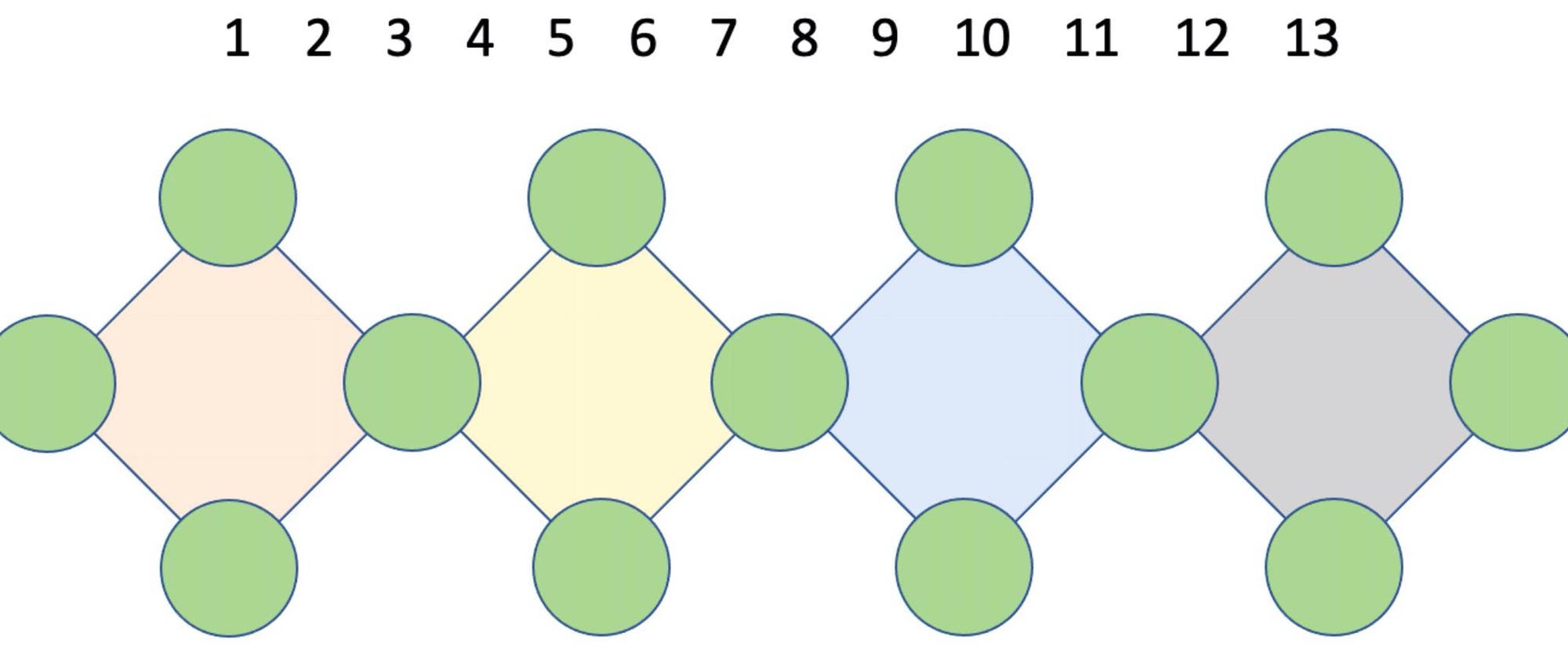
Die Zahlen von 1 bis 13 sollen auf die Kreise verteilt werden, wobei jede der Zahlen genau einmal vorkommen muss. Addiert man die vier Zahlen in den Quadratecken, soll bei allen vier Quadraten der Wert 26 herauskommen.
Wie muss man die 13 Zahlen verteilen?
Eine der Lösungen zeigt die Grafik:
Erklärung
Um diese Aufgabe zu meistern, hilft die folgende Überlegung: Wenn in jedem Dreieck der Summenwert 26 betragen muss, dann ist der Wert der Gesamtsumme 4 mal 26 = 104.
Die Zahlen von 1 bis 13 dürfen aber nur jeweils genau einmal vorkommen und haben einen Summenwert von 91. Also müssen die drei Kreise, die jeweils in zwei Quadraten gezählt werden und damit doppelt zur Gesamtsumme von 104 beitragen, zusammen den Wert 104 – 91 = 13 haben. In dem Lösungsbeispiel ist 1 + 5 + 7 = 13.
Sind diese drei Zahlen festgelegt, lassen sich die restlichen Werte mit etwas Knobelarbeit leicht finden.
Die weiteren Möglichkeiten für den Summenwert 13 zeigt die Abbildung:

Schreiben Sie uns!
Beitrag schreiben