Hemmes mathematische Rätsel: Ein ungewöhnlicher Würfel
1970 veröffentlichte der 1929 geborene amerikanische Maschinenbauingenieur Aaron J. Friedland in New York ein schmales Buch mit dem Titel »Puzzles in Math and Logic«. Es ist eine wunderbare Sammlung von 100 selbst erfundenen Rätseln. Das Büchlein war so erfolgreich, dass es immer wieder neu aufgelegt wurde und noch heute im Buchhandel erhältlich ist. Aaron J. Friedland starb am 1. Mai 2007. Aus seinem Buch stammt das folgende kleine Problem:
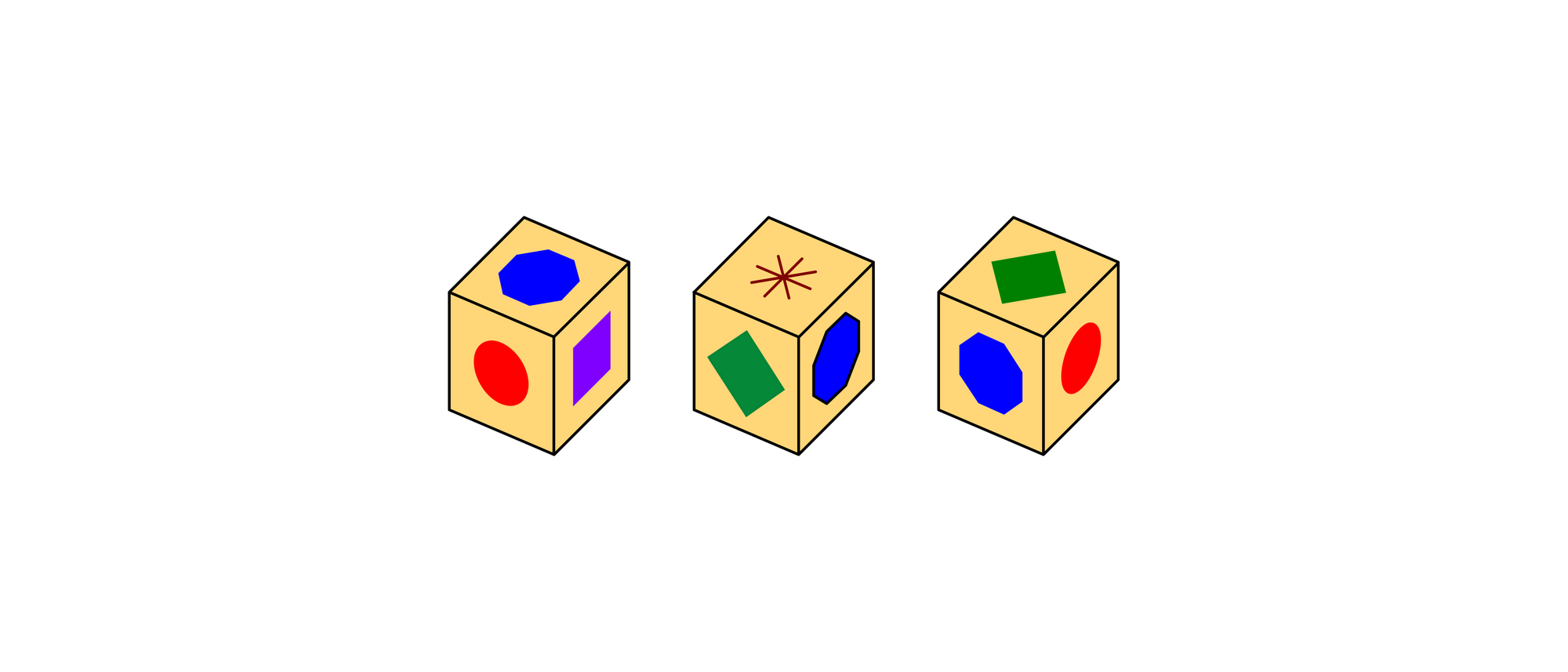
Alle drei Abbildungen zeigen denselben Würfel. Wie sieht die Unterseite des Würfels in der ersten Abbildung aus?
Wenn man in Gedanken den Würfel in der dritten Abbildung so dreht, dass die Seiten mit dem Achteck und der Raute so liegen wie in der zweiten Abbildung, dann sieht man auf der oberen Seite einen Kreis. In der zweiten Abbildung liegt auf der oberen Würfelfläche jedoch ein Stern. Diesen Widerspruch kann man nur auflösen, wenn man annimmt, dass es entweder zwei Achtecke oder zwei Rauten gibt.
Gäbe es zwei Rauten, würden auch in der zweiten und dritten Abbildung an die Fläche mit dem Achteck zwei Flächen mit Rauten, eine Fläche mit einem Stern und eine Fläche mit einem Kreis grenzen. Das ist jedoch nicht möglich, da nach der ersten Abbildung eine der vier an die Fläche mit dem Achteck grenzenden Seiten ein Quadrat zeigt. Folglich kommt nicht die Raute, sondern das Achteck doppelt vor. Der Rest ist jetzt einfach. Die Zeichnung zeigt eine Abwicklung des Würfels. Die untere Seite des Würfels in der ersten Abbildung trägt also ein Achteck.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.