Hemmes mathematische Rätsel: Münzen auf dem Bierdeckel
Ivan Moscovich wurde 1926 in Novi Sad im ehemaligen Jugoslawien als Kind ungarischer Eltern geboren. Sein Vater wurde im 2. Weltkrieg ermordet und er selbst in verschiedenen Konzentrationslagern gefangen gehalten. Nach dem Krieg studierte er Maschinenbau und wanderte nach Israel aus. Dort gründete er 1959 in Tel Aviv das Museum of Science and Technology und wurde dessen erster Direktor.
Ivan Moscovich ist auch ein bekannter Puzzleexperte und hat im Laufe seines Lebens über 5000 Knobeleien gesammelt. Moscovich hat rund 40 Bücher über mathematischen Denksport geschrieben, die in über ein Dutzend Sprachen übersetzt worden sind. Sein bekanntestes Werk ist seine zwölfbändige, durchgängig farbig illustrierte »Mastermind Collection«. Leider ist sie nicht in Deutsch erhältlich. Aus dem im Jahre 2004 erschienenen vierten Band dieser Reihe, der den Titel »The Shoelace Problem & Other Problems« trägt, stammt das folgende geometrische Problem.
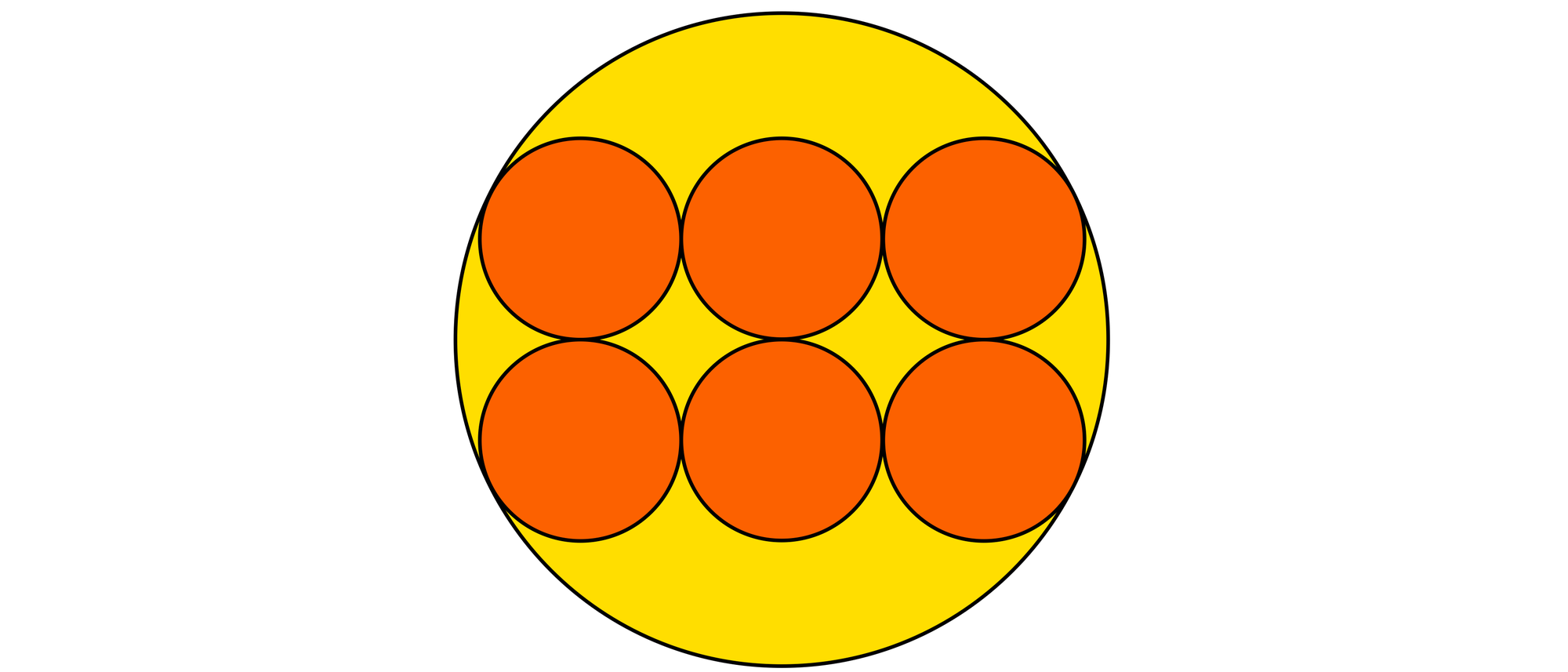
Sechs gleiche Münzen liegen, so wie es die Abbildung zeigt, auf einem Bierdeckel. Wie groß ist das Verhältnis aus Bierdeckelradius und Münzdurchmesser?
Das Dreieck ABC ist rechtwinklig und seine Katheten haben die Längen r und 2r, wobei mit r der Radius der Münzen gemeint ist. Die Hypotenuse BC des Dreiecks lässt sich mit dem Satz des Pythagoras zu BC = r√5 berechnen. Die Strecke CD ist ein Münzradius. Folglich hat der Bierdeckel den Radius R = r√5 + r = (√5 + 1)r. In dieser Gleichung wird der Münzradius durch Münzdurchmesser d ersetzt und man erhält R = (√5 + 1)d/2.
Das gesuchte Verhältnis aus Bierdeckelradius und Münzdurchmesser beträgt folglich R/d = 1⁄2(√5 + 1) ≈ 1,618. Diese Zahl ist der berühmte Goldene Schnitt, der seit der Antike an vielen Stellen in der Mathematik und der Kunst auftaucht. Beispielsweise liegt er den Proportionen vieler Gebäude der griechischen Antike zugrunde.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.