Oktaeder im allgemeinen Tetraeder
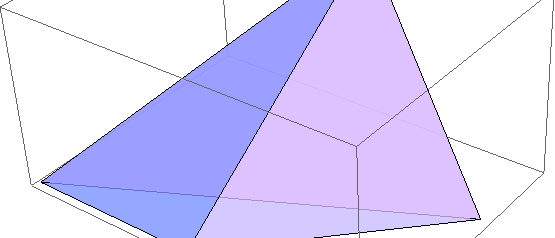
Ein (beliebig unregelmäßiges) Tetraeder hat 6 Kanten. Setzen Sie in dessen "Mitte" ein Oktaeder, indem Sie als dessen Ecken die Kantenmittelpunkte des Tetraeders nehmen. Was kann man über dieses Oktaeder sagen?
Mittelparallelen in Dreiecken.
Zunächst ist klar, dass 6 Kanten 6 Mittelpunkte haben. Diese Mittelpunkte bilden die Ecken eines Oktaeders. Dieses ist ebenfalls unregelmäßig, aber vielleicht nicht ganz so sehr.
Im letzten Rätsel haben wir gezeigt, dass sich der Schwerpunkt eines Tetraeders mitten zwischen den Mitten zweier gegenüberliegender Kanten befindet. Deshalb müssen sich alle drei Diagonalen des Oktaeders in einem Punkt treffen und gegenseitig halbieren. Damit ist dieses schon durch eine beachtliche Symmetrie ausgezeichnet, nämlich Punktsymmetrie bezüglich des Mittelpunktes (von ihm selbst und auch vom Tetraeder).
Gegenüberliegende Seiten des Oktaeders sind deckungsgleich, und die Kanten bilden jeweils zu viert ein Parallelogramm, also drei Stück. Das Oktaeder ist also ein Parallelo-Oktaeder: Jeweils zwei gegenüberliegende Kanten sind gleich lang und parallel zueinander, nämlich halb so lang wie die Tetraederkante, von der sie abstammen, und auch parallel zu ihr. Da alle 6 Tetraederkanten verschieden lang sein können, hat das Oktaeder auch (bis zu) 6 verschiedene Längen bei seinen 12 Kanten.
Wir wollen nun das Tetraeder etwas regelmäßiger machen, es soll jetzt von 4 deckungsgleichen Dreiecken begrenzt werden. Es wird dann "gleichschenklig" genannt, was durchaus sinnvoll, aber nicht ganz selbsterklärend und vielleicht auch missverständlich ist. Welche zusätzlichen Symmetriemerkmale bekommt dann sein Kantenmitten-Oktaeder?
Das Oktaeder aus den Kantenmitten enthält – wie man leicht anhand der Mittelparallelen in den Dreiecken sehen kann – drei Rauten (also gleichseitige Parallelogramme) als Symmetrieebenen und hat daher aufeinander rechtwinklig stehende Diagonalen. Jede von ihnen steht zugleich rechtwinklig zu den Kanten des Tetraeders, die sie trifft.
Die Schattenwürfe des Oktaeders bei Parallelprojektion in geeigneten Richtungen sind dann Dreiecke bzw. Rechtecke. Alle Flächen des Oktaeders sind deckungsgleich und im Maßstab 1:2 ähnlich zu denen des Tetraeders.
Wer nun der Meinung ist, dass man bei dem Stichwort "gleichschenklig" auch ein Tetraeder aus deckungsgleichen gleichschenkligen Dreiecken nehmen sollte, kann dieses dann (inoffiziell) "doppelt-gleichschenklig" nennen und wieder nach dem Oktaeder darin fragen:
Die gleichschenkligen Dreiecke müssen spitzwinklig sein. Die beiden Tetraederkanten, die von ihren Basen gebildet werden, sind nun windschief-rechtwinklig zu einander, d.h. ihre Parallel-Projektion beim Blick in Richtung auf ihrem gemeinsamen Lot (das zugleich eine Oktaeder-Diagonale ist) kreuzen sich rechtwinklig.
Quer zu dieser Diagonalen hat das Tetraeder ebenso wie das Oktaeder eine quadratische Schnittfläche durch den (gemeinsamen) Mittelpunkt, und die anderen Schnittflächen parallel zu dieser sind rechteckig.
Der Vollständigkeit halber wollen wir uns nun noch das reguläre Tetraeder und sein Innenleben ansehen, obwohl es da nun keine Überraschungen mehr gibt:
Das Oktaeder ist nun selbstverständlich auch regulär, alle seine Kanten und Dreiecke sind halb so lang wie die des Tetraeders, und es gibt drei quadratische Schnittflächen durch beide.
So schön auch vollkommene Symmetrie sein mag: Den erstaunlichen Symmetrievorsprung des Kantenmitten-Oktaeders vor dem mehr oder weniger speziellen Tetraeder, zu dem es gehört, finde ich eigentlich spannender. Geht Ihnen das auch so?
Wenn Sie noch (viel) mehr über Tetraeder wissen wollen, empfehle ich die "Modern Pure Solid Geometry" von Nathan Altshiller Court.
Schreiben Sie uns!
Beitrag schreiben