Ptolemaios im Fünfeck
Nach dem Satz von Ptolemäus (siehe auch Rätsel 180) gilt für ein Sehnenviereck (also ein Viereck mit einem Umkreis) mit den Seiten \(a\), \(b\), \(c\) und \(d\) und den Diagonalen \(e\) und \(f\): \(ac + bd = ef\).
Bestimmen Sie daraus bitte die Länge der Diagonalen im regelmäßigen Fünfeck mit der Seitenlänge \(a\).
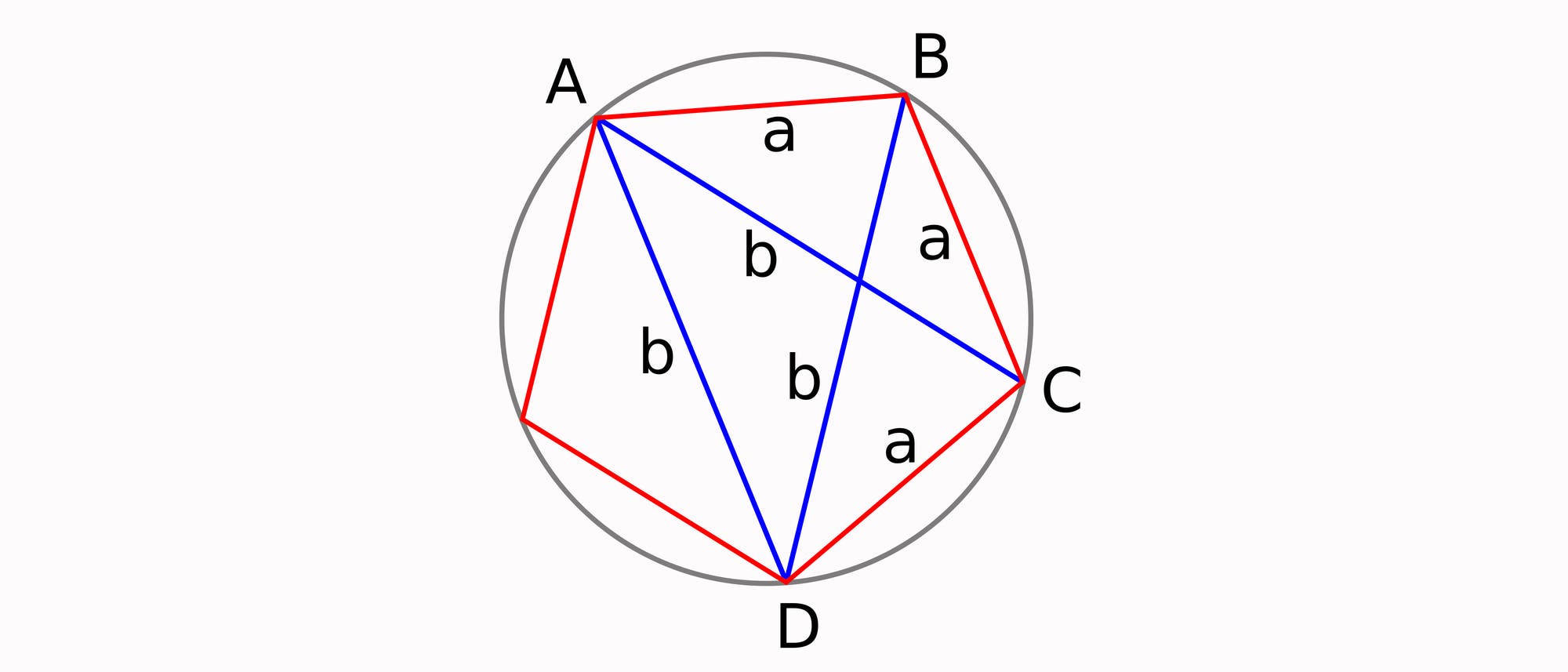
Eine Diagonale im regelmäßigen Fünfeck bildet mit drei von dessen Seiten ein Trapez mit den Seiten \(a,\ a,\ a,\ b\). Die Diagonalen \(b\) dieses Trapezes sind aber ihrerseits auch Diagonalen des Fünfecks.
Da das Trapez gleichschenklig ist (weil seine Ecken die des regelmäßigen Fünfecks sind), gibt es einen Umkreis, und es gilt der Satz von Ptolemäus: \(ab + a^2 = b^2\). Mit der Kenntnis, dass \(b\) größer ist als \(a\), erhält man die Lösung \[\frac{b}{a} = \frac{1+\sqrt{5}}{2} = 1,618...\; ,\] also den goldenen Schnitt.
Dieses geheimnisumwitterte Zahlenverhältnis kreuzt immer auf, wenn man es mit einem regelmäßigen Fünfeck zu tun hat, und gehört zu diesem, etwa so wie \(\sqrt{2}\) zum Quadrat.
Schreiben Sie uns!
Beitrag schreiben