Pythagoras mit Dreh
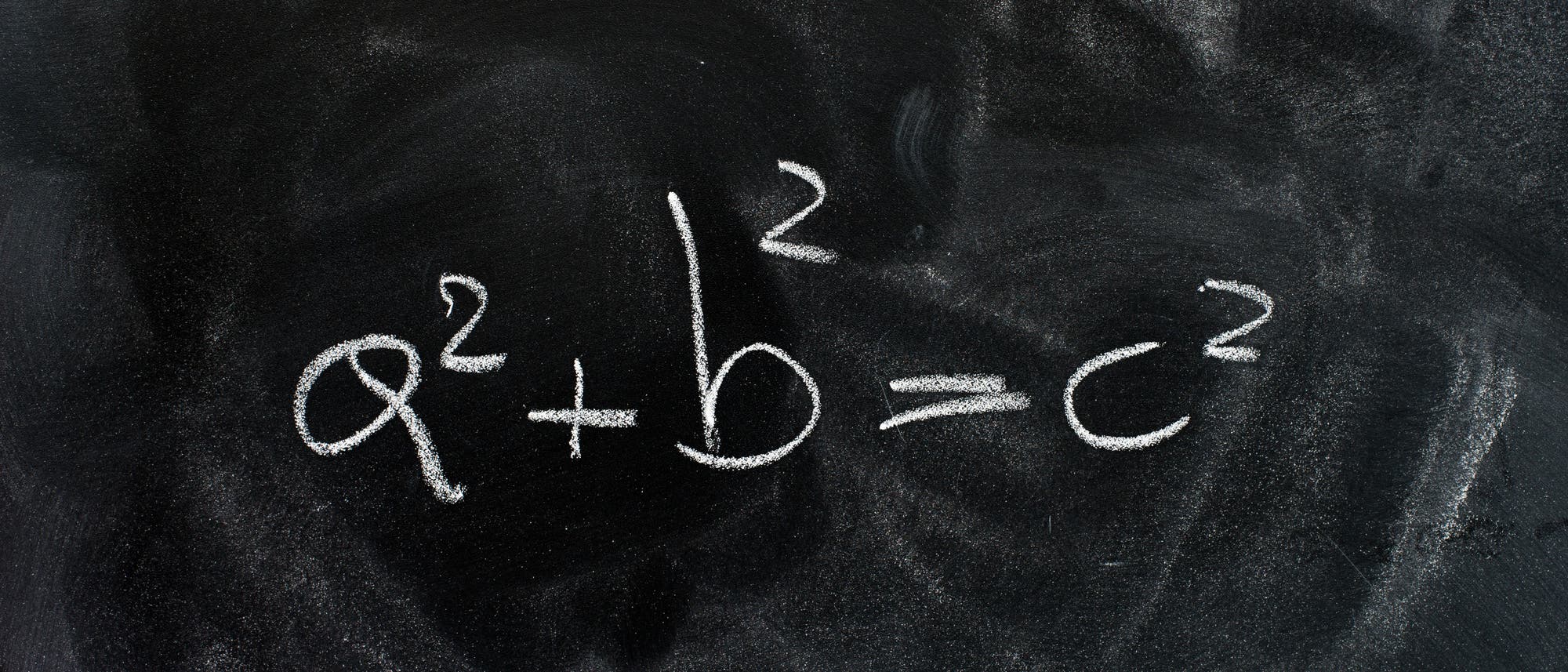
© iStock / fabioderby (Ausschnitt)
Versuchen Sie den Satz des Pythagoras auf kreative Art zu beweisen. Dazu schneiden Sie zwei (deckungsgleiche) Exemplare eines rechtwinkligen Dreiecks aus. Dann sollen die Quadrate über den Katheten zusammen dieselbe Fläche haben wie das Quadrat über der Hypotenuse, und man soll es der Figur ansehen. Gesucht ist eine dritte Figur, die Sie an ihren Ecken mit den zwei Dreiecken verbinden, dass durch Drehen (ohne Überlappung) einmal die beiden kleinen Quadrate entstehen und einmal das große.
Die beiden kleineren Quadrate liegen so aneinander, dass sie eine Ecke und einen Teil einer Seite gemeinsam haben.
Das Quadrat der Hypotenuse des Dreiecks ist in der Animation rot markiert, die Quadrate der Kathete und Ankathete sind schwarz. In der Animation erkennt man deutlich den Satz des Pythagoras.
Schreiben Sie uns!
Beitrag schreiben