Quadrat- und Dreieckszahlen
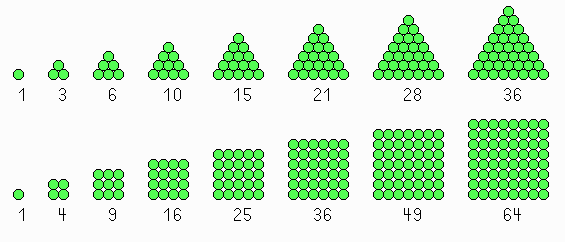
Quadratzahlen haben die Form \(n^2\) (klar), und Dreieckszahlen? Haben die Form \(n(n+1)/2\). Aber schöner ist es, das Problem auf geometrischem Weg zu lösen.
Auch Rauten zeigen Quadratzahlen.
Geht man der Reihe nach von einer Dreieckszahl zur nächsten, so wechselt abwechselnd die Quadratzahl und die (doppelt zunehmende) Dreieckszahl zur nächst höheren:
- 0 = 0 + 2\(\cdot\)0
- 1 = 1 + 2\(\cdot\)0
- 3 = 1 + 2\(\cdot\)1
- 6 = 4 + 2\(\cdot\)1
- 10 = 4 + 2\(\cdot\)3
- 15 = 9 + 2\(\cdot\)3
- 21 = 9 + 2\(\cdot\)6
- 28 = 16 + 2\(\cdot\)6
- 36 = 16 + 2\(\cdot\)10
- 45 = 25 + 2\(\cdot\)10
- 55 = 25 + 2\(\cdot\)15
- 66 = 36 + 2\(\cdot\)15
- usw.
Man kann die Sache natürlich auch algebraisch erledigen, muss dann allerdings zwischen Dreieckszahlen zu geradem und zu ungeradem \(n\) unterscheiden. Mit \(D(n)= n(n+1)/2\) sei die Dreieckszahl zu \(n\) bezeichnet. \[D(n)= {n(n+1)\over 2} = \cases { \left( {n \over 2}\right)^2 + 2 { {n \over 2}\left({n \over 2} +1\right) \over 2} = \left( {n \over 2}\right)^2 + 2 D\left({n \over 2}\right)& für \(n\) gerade \cr \phantom{n} & \cr \left( {n+1 \over 2}\right)^2 + 2 {\left({n-1 \over 2}\right)\left({n+1 \over 2}\right)\over 2} = \left( {n+1 \over 2}\right)^2 + 2 D\left({n-1 \over 2}\right) & für \(n\) ungerade }\] wie man durch Ausmultiplizieren bestätigt.
Können Sie im Kopf eine Dreieckszahl mit 100 Dezimalstellen hinschreiben?
Wie Carl Friedrich Gauß schon als kleiner Junge erkannt hat, ist die Summe der Zahlen von 1 bis 100 das 50-fache von 101 (nämlich von 1 + 100 = 2 + 99 = ... = 50 + 51), also 5050.
Nach dem gleichen Schema geht es mühelos weiter:
55 = 1 + .. + 10
5050 = 1 + .. + 100
500500 = 1 + .. + 1000
50005000 = 1 + .. + 10000
5000050000 = 1 + .. + 100000
500000500000 = 1 + .. + 1000000
50000005000000 = 1 + .. + 10000000
500000005000000 = 1 + .. + 100000000
Schreiben Sie uns!
Beitrag schreiben