Hemmes mathematische Rätsel: Quadrate und Diagonalen
Der Internationale Städtewettbewerb Mathematik wird seit 1979 von Moskau aus organisiert. Er bietet Schülerinnen und Schülern die Möglichkeit, sich mit anspruchsvollen mathematischen Problemen auseinanderzusetzen – in Moskau, in Hamburg und in mehr als 100 anderen Städten der Welt.
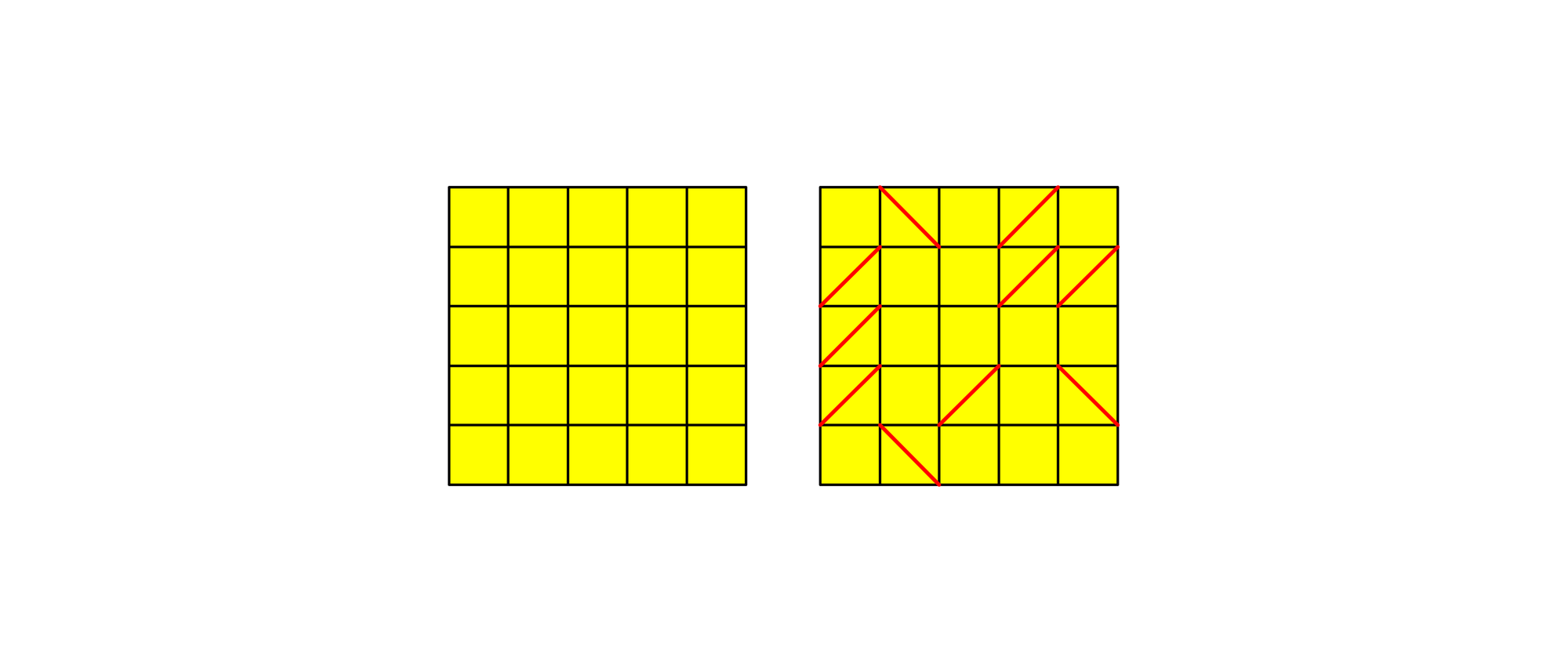
Bei einer der Aufgaben aus dem Jahr 1998 sollen möglichst viele Diagonalen in die 25 Quadrate eines 5×5-feldigen Rasters gezeichnet werden. Allerdings darf jedes Quadrat nur eine Diagonale enthalten, und die Diagonalen dürfen mit ihren Endpunkten nicht auf die Endpunkte anderer Diagonalen treffen. Die linke Abbildung zeigt ein leeres Raster, die rechte ein Beispiel für das Vorgehen, in das sich jedoch weitere Diagonalen einzeichnen lassen. Wie viele Diagonalen lassen sich höchstens in das Raster zeichnen?
Die meisten Menschen, denen ich diese Aufgabe stelle, können fünfzehn Diagonalen in dem Raster unterbringen und sind auch davon überzeugt, die richtige Lösung gefunden zu haben. Man kann aber überraschenderweise sogar sechzehn Diagonalen einzeichnen. Die windmühlenartige Lösung ist, abgesehen von ihrem Spiegelbild, eindeutig.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.