Rabinowitz
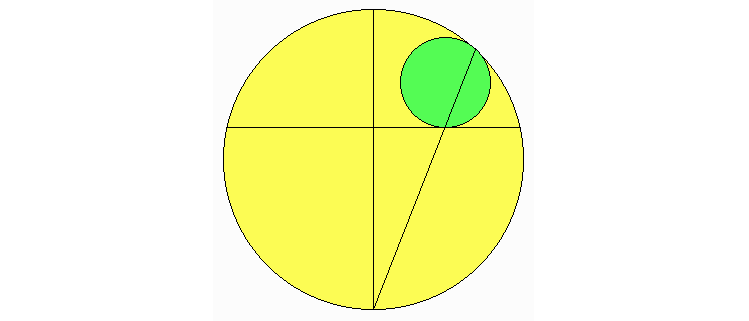
Der kleine Kreis berührt den großen und eine waagerechte Sehne, die rechtwinklig zu dem eingezeichneten Durchmesser liegt. Zeigen Sie bitte, dass das untere Ende des Durchmessers und die beiden Berührpunkte des kleinen Kreises (mit dem großen Kreis und der Sehne) immer auf einer Geraden liegen.
Hierzu eine Animation (ohne Lösung):
Ähnliche Dreiecke.
Ross Honsberger gibt in seinen "Footsteps" auf Seite 30 Stanley Rabinowitz aus Nashua (New Hampshire) als Quelle (für Aufgabe und Lösung) an: Problem 1070 in Crux Mathematicorum 1987, 31, dort dreidimensional.
Übrigens gibt es noch eine zweite Sehne, sie gehört zum anderen Ende des Durchmessers.
Schreiben Sie uns!
Beitrag schreiben