Rauten im Zwölfeck
© Norbert Treitz (Ausschnitt)
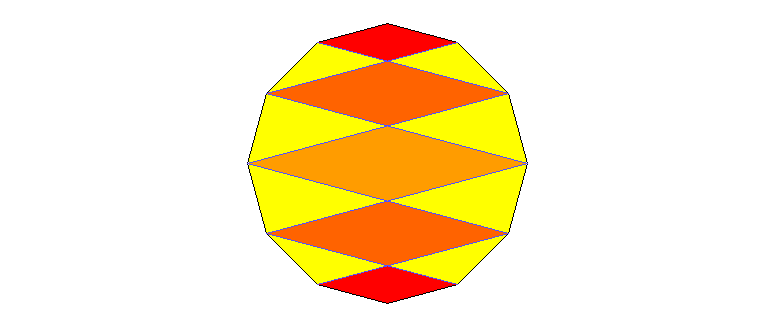
Wie verhalten sich die Flächen der Rauten in diesem regelmäßigen Zwölfeck zueinander?
Besonders einfach sieht man es in einem quadratischen Raster mit dem halben Umkreisradius als Einheit.
© Norbert Treitz (Ausschnitt)
Jedes gleichseitige Dreieck (und damit auch das in verschiedenen Grüntönen hervorgehobene) hat als Verhältnis von Höhe zu Grundseite den Wert \(\sqrt3/2\). Da die Rhomben alle ähnlich zueinander sind, verhalten sich ihre Flächen wie die Quadrate entsprechender Seiten oder Diagonalen.
Die horizontale halbe Diagonale der kleinsten Raute hat die Länge 1, die der zweitgrößten Raute \(\sqrt3/2\) und die der größten Raute die Länge 2. Durch Quadrieren kommt man von den Längen- auf die Flächenverhältnisse. Demnach lautet die Antwort 1:3:4:3:1.
Schreiben Sie uns!
Beitrag schreiben