Robervals Pteroide
© Spektrum der Wissenschaft (Ausschnitt)
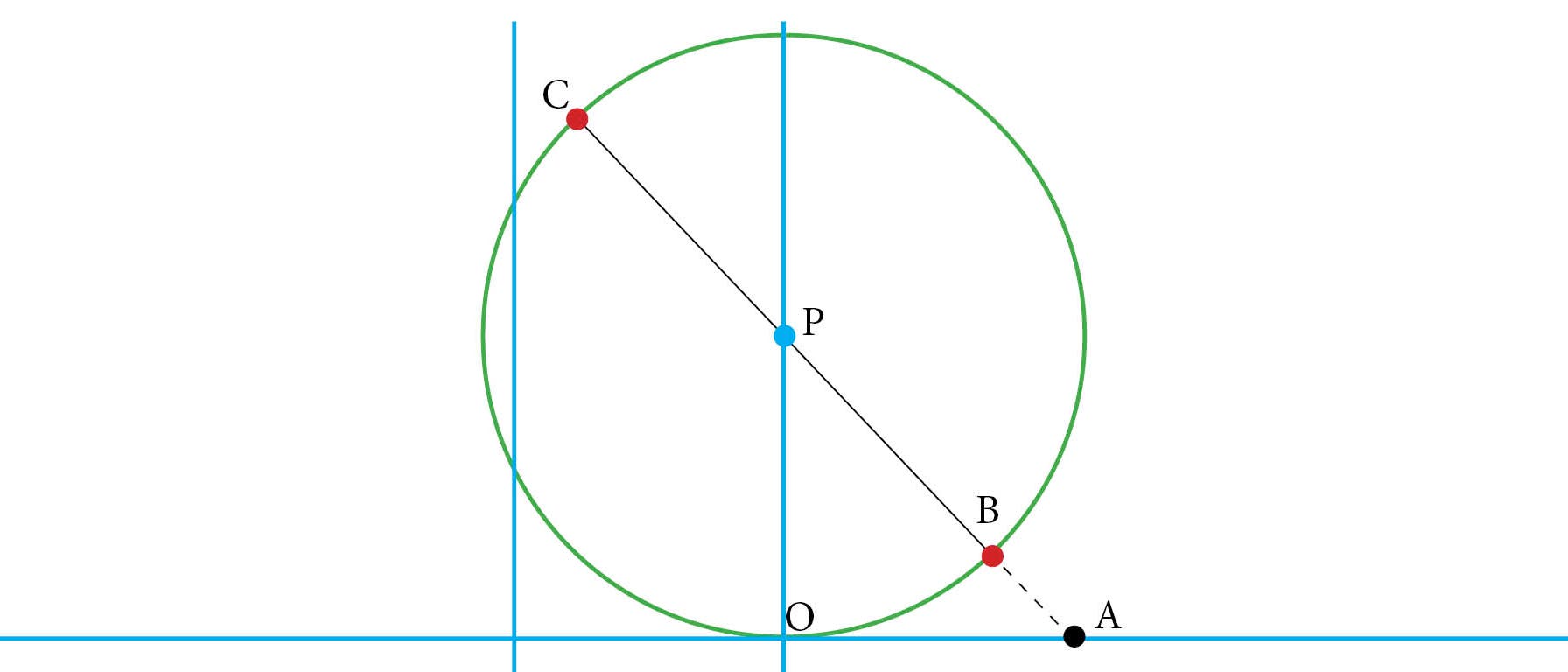
In dem obigen Bild sind nur die blauen Linien und der Punkt \(A\) fest verankert. Die restlichen Punkte und der Kreis stellen nur eine Art Momentaufnahme dar.
Man zeichne eine beliebige Gerade (schwarz) vom Punkt \(A\)aus. Sie schneidet die feste (hier blaue vertikale) Gerade im Punkt \(P\). Auf der schwarzen Gerade trage man von \(P\) aus Strecken der Länge \(PO\) ab, nämlich \(PB\) und \(PC\). Wenn man die schwarze Gerade variiert, laufen \(B\) und \(C\) auf einer Kurve, die Gilles Personne de Roberval (1602–1675) 1645 "Pteroide" (Flügelkurve) nannte, die aber heute als "gerade Strophoide" bezeichnet wird. Wie sieht sie aus?
Schreiben Sie uns!
Beitrag schreiben