Schneeflöckchen
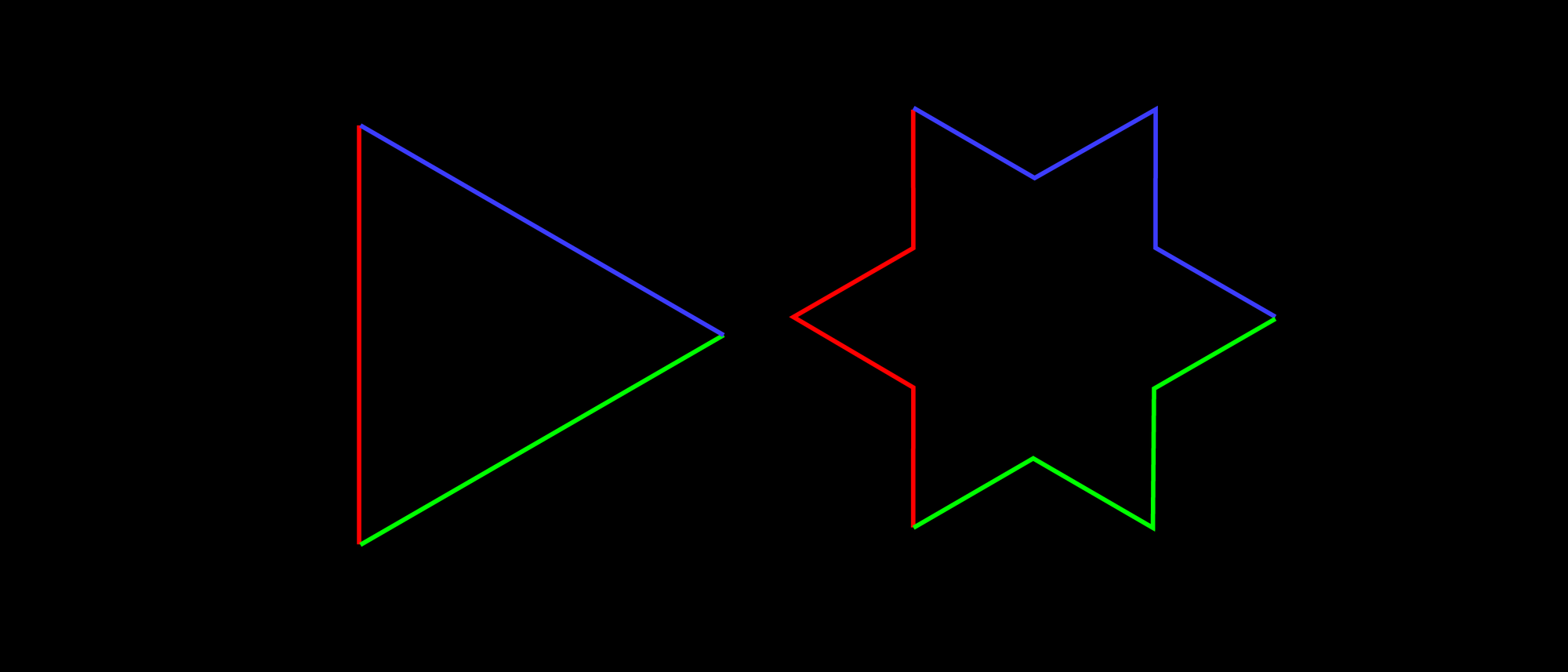
Hier ist bei einem gleichseitigen Dreieck jede Seite durch einen Streckenzug aus 4 Teilen von 1/3 der Länge ersetzt, und zwar immer nach außen. Das kann man "beliebig" fein fortsetzen. Was kann man über den Umfang und über den Flächeninhalt sagen?
Es ist die Schneeflockenkurve von Helge von Koch. Im Rahmen unserer Bildauflösung sehen sie und ihre Vorläufer so aus:
Die Fläche ist offenbar durch die des umgebenden Sechsecks beschränkt, also sicher endlich. Der Umfang nimmt dagegen bei jedem Verfeinerungsschritt mit dem Faktor 4/3 zu, wächst also geometrisch gegen Unendlich.
Was geschieht, wenn man die Zacken nach innen macht?Wenn wir uns vorstellen, dass wir mit Linksabbiegen (gegen den Uhrzeigersinn) um das große Dreieck fahren und dabei alle kleinen Zacken nach links ansetzen, sieht das so aus:
Die Länge des Umfangs wächst wie zuvor, aber die Fläche ist kleiner, schrumpft aber offenbar nicht gegen 0. Wir können auch abwechselnd in der einen Verfeinerungsstufe nach links und in der nächsten nach rechts ausweichen:
Wie sieht es aus, wenn wir von einem Quadrat ausgehen und alle Strecken mit rechtwinkligen Umwegen verzieren?
Zunächst sehen wir uns Quadrate nach außen an:
Und nun abwechselnd:
Wir können auch eine "rechtwinklige Zickzackkurve" einsetzen:
Schreiben Sie uns!
Beitrag schreiben